题目内容
函数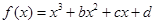 的大致图象如图所示,则
的大致图象如图所示,则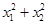 等于( )
等于( )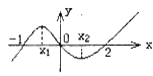
A.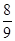 | B.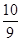 | C.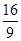 | D.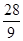 |
C
解析试题分析:由图可得函数f(x)的三个零点是-1、0、2,建立方程解得b=-1,c=-2,d=0,然后利用导数求出函数f(x)的极值点即可求出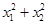 .
.
考点:1.函数的零点;2.函数的极值.

练习册系列答案
相关题目
定义在R上的函数 满足:
满足: 恒成立,若
恒成立,若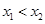 ,则
,则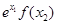 与
与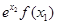 的大小关系为 ( )
的大小关系为 ( )
A. 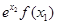 | B.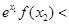 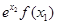 |
C.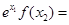 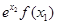 | D.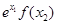 与 与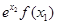 的大小关系不确定 的大小关系不确定 |
等差数列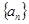 中的
中的 是函数
是函数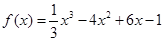 的极值点,则
的极值点,则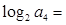 ( )
( )
A.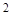 | B.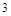 | C.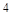 | D.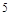 |
曲线y=cosx(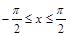 )与两坐标轴所围成的图形的面积为( )
)与两坐标轴所围成的图形的面积为( )
| A.4 | B.2 | C.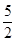 | D.3 |
设函数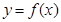 在(0,+
在(0,+ )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数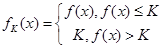 ,取函数
,取函数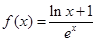 ,恒有
,恒有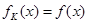 ,则( )
,则( )
A.K的最大值为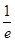 | B.K的最小值为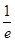 |
| C.K的最大值为2 | D.K的最小值为2 |
已知函数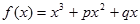 与
与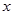 轴相切于
轴相切于 点,且极小值为
点,且极小值为 ,则
,则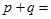 ( )
( )
| A.12 | B.15 | C.13 | D.16 |
已知e为自然对数的底数,则函数y=xex的单调递增区间是( )
| A.[-1,+∞) | B.(-∞,-1] |
| C.[1,+∞) | D.(-∞,1] |
设函数f(x)=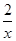 +ln x,则( ).
+ln x,则( ).
A.x= 为f(x)的极大值点 为f(x)的极大值点 | B.x= 为f(x)的极小值点 为f(x)的极小值点 |
| C.x=2为f(x)的极大值点 | D.x=2为f(x)的极小值点 |
直线y=kx+b与曲线y=x3+ax+1相切于点(2,3),则b的值为( ).
| A.-3 | B.9 | C.-15 | D.-7 |