题目内容
(本题满分12分)
已知椭圆的中心在原点,焦点在x轴上,长轴长是短轴长的2倍且经过点M(2,1),平行于OM的直线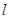 在y轴上的截距为m(m≠0),
在y轴上的截距为m(m≠0),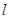 交椭圆于A、B两个不同点。
交椭圆于A、B两个不同点。
(1)求椭圆的方程;
(2)求m的取值范围;
(3)求证直线MA、MB与x轴始终围成一个等腰三角形.
【答案】
(1) ;(2)
;(2)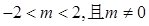 ;
;
(3)直线MA、MB与x轴始终围成一个等腰三角形。
【解析】
试题分析:(1)先设出椭圆的标准方程,根据题意联立方程组,求得a和b,椭圆的方程可得.
(2)由点斜式设出直线l的方程与椭圆方程联立消去y,根据判别式大于0求得k的范围.
(3)设A(x1,y1),B(x2,y2)由根据韦达定理,分别求得x1+x2和x1x2进而表示出k1和k2,进而可求得k1+k2.从而确定三角形为等腰三角形。
解:(1)设椭圆方程为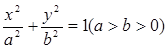
则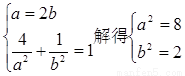 ∴椭圆方程为
∴椭圆方程为
(2)∵直线l平行于OM,且在y轴上的截距为m ; 又KOM=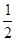
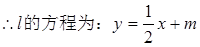
由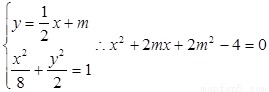
∵直线l与椭圆交于A、B两个不同点,
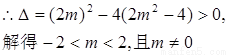
(3)设直线MA、MB的斜率分别为k1,k2,只需证明k1+k2=0即可
设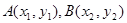 则
则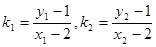
由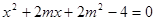 可得
可得 
而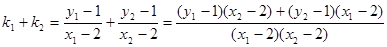
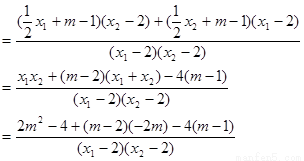
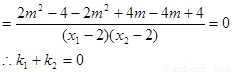
故直线MA、MB与x轴始终围成一个等腰三角形。
考点:本试题主要考查了椭圆的应用.考查了学生综合分析问题和解决问题的能力.
点评:对于解析几何问题关键是要设出直线方程并能利用设而不求的思想和韦达定理得到要求解的关系式,使我们必须要用到的重要的思想方法。

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面