题目内容
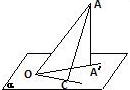 AC是平面a的斜线,且AO=a,AO与a成60°角,OC?a,AA'⊥a于A',∠A'OC=45°,则A到直线OC的距离是
AC是平面a的斜线,且AO=a,AO与a成60°角,OC?a,AA'⊥a于A',∠A'OC=45°,则A到直线OC的距离是分析:如图可知cos∠AOA′=cos∠A′OC=cos∠AOC,进而求得cos∠AOC,利用直角三角形AOC求得A到直线OC的距离,求得答案.
解答:解:∵cos∠AOA′•cos∠A′OC=cos∠AOC,
∴
•
=cos∠AOC.
∴cos∠AOC=
.
∴sin∠AOC=
,
∴AC=AO•sin∠∠AOC=a×
=
a.
故答案为:
a;
.
∴
| 1 |
| 2 |
| ||
| 2 |
∴cos∠AOC=
| ||
| 4 |
∴sin∠AOC=
| ||
| 4 |
∴AC=AO•sin∠∠AOC=a×
| ||
| 4 |
| ||
| 4 |
故答案为:
| ||
| 4 |
| ||
| 4 |
点评:本题主要考查了点到直线的距离计算.在立体几何中,求点到直线的距离是一个常见的题型,属于基础题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
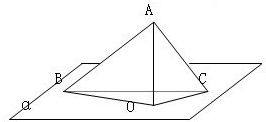 如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=
如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=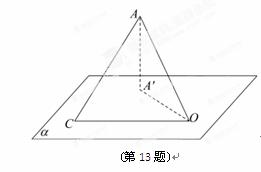
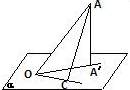
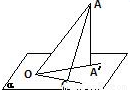 AC是平面a的斜线,且AO=a,AO与a成60°角,OCÌa,AA'⊥a于A',∠A'OC=45°,则A到直线OC的距离是 ,∠AOC的余弦值是 .
AC是平面a的斜线,且AO=a,AO与a成60°角,OCÌa,AA'⊥a于A',∠A'OC=45°,则A到直线OC的距离是 ,∠AOC的余弦值是 .