题目内容
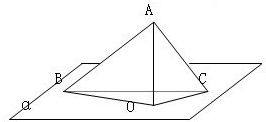 如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=
如图所示,A∉平面α,AB、AC是平面α的两条斜线,O是A在平面α内的射影,AO=4,OC=| 3 |
| 15 |
| 15 |
分析:利用勾定理,根据已知,先求出△ABC的三边长,利用余弦定理求出B角的余弦,进而根据平方关系求出B的正弦,结合C到AB的距离为BC•sinB得到答案.
解答:解:在Rt△AOB中,
∵AO=4,∠OBA=30°,
∴AB=8,OB=4
∵BO⊥OC,
在Rt△BOC中,由OC=
,
∴BC=
在Rt△AOC中,AC=
在△ABC中,cosB=
=
∴sinB=
则C到AB的距离为BC•sinB=
•
=
故答案为:
∵AO=4,∠OBA=30°,
∴AB=8,OB=4
| 3 |
∵BO⊥OC,
在Rt△BOC中,由OC=
| 3 |
∴BC=
| 51 |
在Rt△AOC中,AC=
| 19 |
在△ABC中,cosB=
|
2
| ||
| 17 |
∴sinB=
| ||
| 17 |
则C到AB的距离为BC•sinB=
| 51 |
| ||
| 17 |
| 15 |
故答案为:
| 15 |
点评:本题考查的知识点是点到线的距离,其中将空间问题转化为平面解三角形问题是解答的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
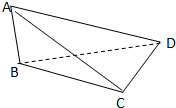 如图所示,AB⊥平面BCD,∠BCD=90°则图中互相垂直的平面有( )
如图所示,AB⊥平面BCD,∠BCD=90°则图中互相垂直的平面有( ) 如图所示,将平面直角坐标系中的纵轴绕点O顺时针旋转300(坐标轴的长度单位不变)构成一个斜坐标系xOy,平面上任一点P关于斜坐标系的坐标(x,y)用如下方式定义:过P作两坐标轴的平行线分别交坐标轴Ox于点M,Oy于点N,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.在斜坐标系中,若A,B两点的坐标分别为(1,2),(-2,3),则线段AB的长为
如图所示,将平面直角坐标系中的纵轴绕点O顺时针旋转300(坐标轴的长度单位不变)构成一个斜坐标系xOy,平面上任一点P关于斜坐标系的坐标(x,y)用如下方式定义:过P作两坐标轴的平行线分别交坐标轴Ox于点M,Oy于点N,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.在斜坐标系中,若A,B两点的坐标分别为(1,2),(-2,3),则线段AB的长为 (2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.
(2012•浦东新区一模)如图所示,在平面直角坐标系xOy上放置一个边长为1的正方形PABC,此正方形PABC沿x轴滚动(向左或向右均可),滚动开始时,点P位于原点处,设顶点P(x,y)的纵坐标与横坐标的函数关系是y=f(x),x∈R,该函数相邻两个零点之间的距离为m.