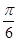题目内容
若函数f(x)=(sinx+cosx)2-2cos2x-m在[0, ]上有零点,则实数m的取值范围为( )
]上有零点,则实数m的取值范围为( )
A.[-1, ] ] | B.[-1,1] |
C.[1, ] ] | D.[- ,-1] ,-1] |
A
解析

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
设函数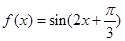 ,则下列结论正确的是
,则下列结论正确的是
A.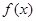 的图像关于直线 的图像关于直线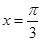 对称 对称 | B.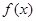 的图像关于点 的图像关于点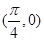 对称 对称 |
C.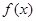 的最小正周期为 的最小正周期为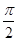 | D.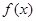 在 在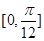 上为增函数 上为增函数 |
函数 的一条对称轴方程是( )
的一条对称轴方程是( )
A. | B. | C. | D. |
若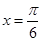 是
是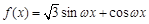 的图象的一条对称轴,则
的图象的一条对称轴,则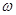 可以是( )
可以是( )
| A.4 | B.8 | C.2 | D.1 |
函数f(x)= cos(3x-θ)-sin(3x-θ)是奇函数,则θ为( )
cos(3x-θ)-sin(3x-θ)是奇函数,则θ为( )
| A.kπ(k∈Z) | B.kπ+ (k∈Z) (k∈Z) |
C.kπ+ (k∈Z) (k∈Z) | D.-kπ- (k∈Z) (k∈Z) |
 等于( )
等于( )
| A.sin2-cos2 | B.cos2-sin2 |
| C.±(sin2-cos2) | D.sin2+cos2 |
若函数f(x)=2sin (-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则(
(-2<x<10)的图像与x轴交于点A,过点A的直线l与函数的图像交于B,C两点,则( +
+ )·
)· =( )
=( )
| A.-32 | B.-16 |
| C.16 | D.32 |
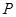 在半径为
在半径为 的半圆上运动,
的半圆上运动, 是直径,当
是直径,当 到
到 运动时,点
运动时,点 与
与 的面积
的面积 的函数
的函数 的图像是下图中的( )
的图像是下图中的( )




 的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P
的图象向右平移φ(φ>0)个单位长度后得到函数g(x)的图象,若f(x),g(x)的图象都经过点P ,则φ的值可以是( )
,则φ的值可以是( )