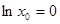题目内容
下列命题中假命题的是( )
| A、?x0∈R,sinx0+cosx0=2 | ||
B、?x∈(0,
| ||
| C、?x∈R,2x>0 | ||
| D、?x0∈R,lnx0=0 |
分析:不存在实数使得这个实数的正弦和余弦值之和等于2,根据正切线可知,当一个角是锐角时,x<tanx成立,根据底数是2的指数函数可知,它的值域是正实数,当自变量取1时,1的对数值是0,得到结果.
解答:解:∵不存在实数使得这个实数的正弦和余弦值之和等于2,故A错误,
根据正切线可知,当一个角是锐角时,x<tanx成立,故B说法正确,
根据底数是2的指数函数可知,它的值域是正实数,故C说法正确,
当自变量取1时,1的对数值是0,
综上可知假命题是A,
故选A.
根据正切线可知,当一个角是锐角时,x<tanx成立,故B说法正确,
根据底数是2的指数函数可知,它的值域是正实数,故C说法正确,
当自变量取1时,1的对数值是0,
综上可知假命题是A,
故选A.
点评:本题考查命题的真假,考查三角函数的值域,考查正切线和弧长的比较,考查指数函数的性质,考查对数函数的性质,是一个综合题目.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
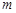 ,
,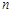 是两条不同直线,
是两条不同直线,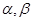 是两个不同平面,则下列命题中假命题的是
是两个不同平面,则下列命题中假命题的是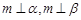 则
则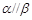
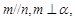 则
则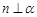
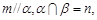 则
则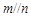
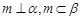 则
则 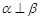
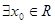 ,
,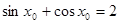 B.
B.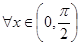 ,
,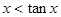
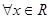 ,
,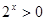 D.
D.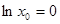
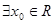 ,
,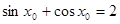 B.
B.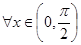 ,
,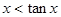
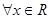 ,
,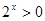 D.
D.