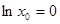题目内容
下列命题中假命题的是( )
①若实数a,b,c,d满足a>b>0,c>d>0,则a2-
>b2-
;
②若实数a,b满足a>b,则(
)a<(
)b;
③若实数a,b满足a>0,b>0,且a2+b2=2,则a+b的最小值为2;
④若实数a,b满足a>0,b>0,且a+b=ab,则ab的最大值为4.
①若实数a,b,c,d满足a>b>0,c>d>0,则a2-
| d |
| c |
②若实数a,b满足a>b,则(
| 1 |
| 3 |
| 1 |
| 3 |
③若实数a,b满足a>0,b>0,且a2+b2=2,则a+b的最小值为2;
④若实数a,b满足a>0,b>0,且a+b=ab,则ab的最大值为4.
分析:①根据不等式的性质进行判断.②根据指数函数单调性进行判断.③根据基本不等式的应用判断.④根据基本不等式的应用判断.
解答: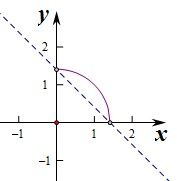 解:①∵a>b>0,c>d>0,∴a2>b2>0,
解:①∵a>b>0,c>d>0,∴a2>b2>0,
>
>0,∴-
>-
,∴a2-
>b2-
成立,∴①为真命题.
②∵函数y=(
)x为减函数,∴当a>b上,则(
)a<(
)b成立,∴②为真命题.
③作出a,b满足条件的图象如图:为圆在第一象限内的部分,设z=a+b,则b=-a+z,则由图象可知z无最小值,∴③为假命题.
④若实数a,b满足a>0,b>0,且a+b=ab,则ab的最大值为4.
④∵a+b=ab≥2
,∴ab≥4,当且仅当a=b=2时取等号,∴④为假命题.
故选:D.
 解:①∵a>b>0,c>d>0,∴a2>b2>0,
解:①∵a>b>0,c>d>0,∴a2>b2>0,| c |
| d |
| d |
| c |
| d |
| c |
②∵函数y=(
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
③作出a,b满足条件的图象如图:为圆在第一象限内的部分,设z=a+b,则b=-a+z,则由图象可知z无最小值,∴③为假命题.
④若实数a,b满足a>0,b>0,且a+b=ab,则ab的最大值为4.
④∵a+b=ab≥2
| ab |
故选:D.
点评:本题主要考查不等式的性质以及应用,要求熟练掌握各种不等式的性质和应用.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
下列命题中假命题的是( )
| A、?x0∈R,sinx0+cosx0=2 | ||
B、?x∈(0,
| ||
| C、?x∈R,2x>0 | ||
| D、?x0∈R,lnx0=0 |
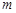 ,
,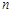 是两条不同直线,
是两条不同直线,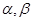 是两个不同平面,则下列命题中假命题的是
是两个不同平面,则下列命题中假命题的是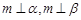 则
则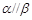
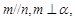 则
则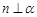
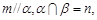 则
则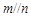
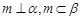 则
则 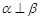
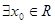 ,
,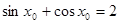 B.
B.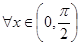 ,
,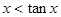
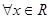 ,
,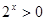 D.
D.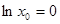
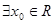 ,
,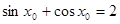 B.
B.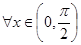 ,
,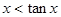
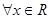 ,
,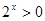 D.
D.