题目内容
y=f(x)是关于x=3对称的奇函数,f(1)=1,cosx-sinx=3
| ||
| 5 |
| 15sin2x | ||
cos(x+
|
分析:由cosx-sinx=
,利用辅助角公式易得cos(x+
)=
,代入易求t的值,又由y=f(x)是关于x=3对称的奇函数,则f(x)是一个周期为6的周期函数,结合f(1)=1即可求出f(t)的值.
3
| ||
| 5 |
| π |
| 4 |
| 3 |
| 5 |
解答:解:∵cosx-sinx=
,
∴cos(x+
)=
又∵sin2x=
,
∴
=7.
又∵函数y=f(x)是关于x=3对称的奇函数,
∴f[
]=f(7)=f(3+4)=f(3-4)=f(-1)=-f(1)=-1.
3
| ||
| 5 |
∴cos(x+
| π |
| 4 |
| 3 |
| 5 |
又∵sin2x=
| 7 |
| 25 |
∴
| 15sin2x | ||
cos(x+
|
又∵函数y=f(x)是关于x=3对称的奇函数,
∴f[
| 15sin2x | ||
cos(x+
|
点评:利用函数的周期性解题要注意:对于任意实数x,①若f(x+T)=f(x),则T为函数的周期;②若f(x+T)=-f(x),则2T为函数的周期;③若(a,y),(b,y)分别为函数的两个对称中心则T=2|(a-b)|④对于任意x∈R,f(x+1)=
,则T=2⑤若(a,y)为函数的对称中心,x=b为函数的对称轴,则T=4|(a-b)|
| 1-f(x) |
| 1+f(x) |

练习册系列答案
相关题目
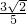 ,若t=
,若t=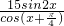 ,则f(t)=________.
,则f(t)=________.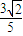 ,若t=
,若t=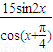 ,则f(t)= .
,则f(t)= .