题目内容
已知△ABC的A(-2,5),B(-5,6),C(7,-4),求:
①AB边上的中线所在的直线方程;
②BC边上的垂直平分线所在的直线方程;
③△ABC中平行于AC边的中位线所在的直线方程,并化为截距式.
【答案】分析:①由题意可得AB的中点为D( ,
, ),进而可得斜率,由点斜式可写方程,化简即可;
),进而可得斜率,由点斜式可写方程,化简即可;
②BC的中点为E(1,1),进而可得斜率,同①可得;
③由①②可知AB的中点为D(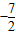 ,
, ),BC的中点为E(1,1),可得斜率,化为截距式即可.
),BC的中点为E(1,1),可得斜率,化为截距式即可.
解答:解:①由题意可得AB的中点为D(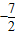 ,
, ),而C(7,-4),
),而C(7,-4),
故所求直线的斜率为 =-
=- ,故方程为y+4=
,故方程为y+4= (x-7),
(x-7),
化成一般式即为19x+21y-49=0;
②BC的中点为E(1,1),而BC的斜率为 =
= ,
,
故其垂直平分线的斜率为 ,故方程为y-1=
,故方程为y-1= (x-1),
(x-1),
化成一般式即为6x-5y-1=0;
③由①②可知AB的中点为D( ,
, ),BC的中点为E(1,1),
),BC的中点为E(1,1),
故所求直线的斜率为 =-1,故方程为y-1=-1(x-1),
=-1,故方程为y-1=-1(x-1),
化为截距式为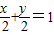
点评:本题考查直线方程的求解,用点斜式写方程是截距问题的基础,属基础题.
 ,
, ),进而可得斜率,由点斜式可写方程,化简即可;
),进而可得斜率,由点斜式可写方程,化简即可;②BC的中点为E(1,1),进而可得斜率,同①可得;
③由①②可知AB的中点为D(
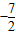 ,
, ),BC的中点为E(1,1),可得斜率,化为截距式即可.
),BC的中点为E(1,1),可得斜率,化为截距式即可.解答:解:①由题意可得AB的中点为D(
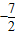 ,
, ),而C(7,-4),
),而C(7,-4),故所求直线的斜率为
 =-
=- ,故方程为y+4=
,故方程为y+4= (x-7),
(x-7),化成一般式即为19x+21y-49=0;
②BC的中点为E(1,1),而BC的斜率为
 =
= ,
,故其垂直平分线的斜率为
 ,故方程为y-1=
,故方程为y-1= (x-1),
(x-1),化成一般式即为6x-5y-1=0;
③由①②可知AB的中点为D(
 ,
, ),BC的中点为E(1,1),
),BC的中点为E(1,1),故所求直线的斜率为
 =-1,故方程为y-1=-1(x-1),
=-1,故方程为y-1=-1(x-1),化为截距式为
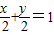
点评:本题考查直线方程的求解,用点斜式写方程是截距问题的基础,属基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
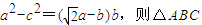 的面积为 .
的面积为 .