题目内容
已知函数f(x)=2sin(ωx),其中常数ω>0
(1)令ω=1,判断函数F(x)=f(x)+f(x+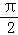 )的奇偶性,并说明理由;
)的奇偶性,并说明理由;
(2)令ω=2,将函数y=f(x)的图象向左平移个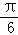 单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
(1)F(x)既不是奇函数,也不是偶函数(2)21或20
解析试题分析:(1)f(x)=2sinx,
F(x)=f(x)+f(x+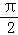 )=2sinx+2sin(x+
)=2sinx+2sin(x+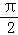 )=2(sinx+cosx),
)=2(sinx+cosx),
F(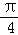 )=2
)=2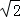 ,F(﹣
,F(﹣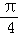 )=0,F(﹣
)=0,F(﹣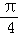 )≠F(
)≠F(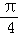 ),F(﹣
),F(﹣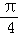 )≠﹣F(
)≠﹣F(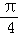 ),
),
所以,F(x)既不是奇函数,也不是偶函数.
(2)f(x)=2sin2x,
将y=f(x)的图象向左平移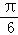 个单位,再向上平移1个单位后得到y=2sin2(x+
个单位,再向上平移1个单位后得到y=2sin2(x+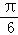 )+1的图象,所以g(x)=2sin2(x+
)+1的图象,所以g(x)=2sin2(x+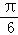 )+1.
)+1.
令g(x)=0,得x=kπ+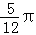 或x=kπ+
或x=kπ+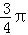 (k∈z),
(k∈z),
因为[a,a+10π]恰含10个周期,所以,当a是零点时,在[a,a+10π]上零点个数21,
当a不是零点时,a+kπ(k∈z)也都不是零点,区间[a+kπ,a+(k+1)π]上恰有两个零点,故在[a,a+10π]上有20个零点.
综上,y=g(x)在[a,a+10π]上零点个数的所有可能值为21或20.
考点:函数y=Asin(ωx+φ)的图象变换;函数奇偶性的判断;根的存在性及根的个数判断
点评:本题考查函数y=Asin(ωx+φ)的图象变换、函数的奇偶性、根的存在性及根的个数的判断,考查数形结合思想,结合图象分析是解决(2)问的关键

练习册系列答案
相关题目
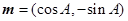 ,
,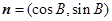 ,
,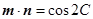 ,其中
,其中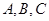 为
为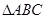 的内角.
的内角.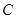 的大小;
的大小;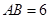 ,且
,且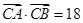 ,求
,求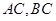 的长.
的长.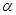 为第三象限角,
为第三象限角,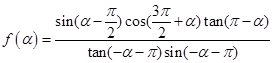 .
.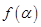 (2)若
(2)若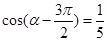 ,求
,求 ,
, .
. 的最大值和最小值;
的最大值和最小值; 在
在 的取值范围.
的取值范围.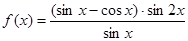
 的定义域及最小正周期;
的定义域及最小正周期;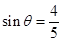 ,
,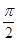 <θ<π.
<θ<π. 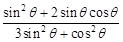 的值.
的值. (
( )的部分图像如右所示.
)的部分图像如右所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的值.
的值. 
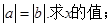
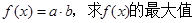
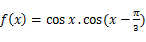
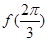 的值;
的值;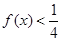 成立的x的取值集合
成立的x的取值集合