题目内容
设直线l与球O有且只有一个公共点P，从直线l出发的两个半平面α，β截球O的两个截面圆的半径分别为1和
，二面角α-l-β的平面角为
，则球O的表面积为（ ）
| 3 |
| π |
| 2 |
分析：设两个半平面α，β截球O的两个截面圆的圆心分别为O1，02，根据球的截面圆性质及球的切线性质得OO1⊥α，OO2⊥β．OP⊥l，继而四边形O102OP为矩形，得出O1P2+O2P2=OP2=R2，再计算球O的表面积即可．
解答：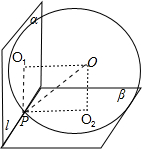
解：设两个半平面α，β截球O的两个截面圆的圆心分别为O1，02，连接O1P，O2P，OP，如图所示
由球的截面圆性质及球的切线性质得OO1⊥α，OO2⊥β．OP⊥l，且O1P=1，O2P=
，
∴l⊥面OO1P，l⊥面OO2P，∴O1，02，O，P四点共面，
∠O1PO2 为二面角α-l-β的平面角，∠O1PO2=
，四边形O102OP为矩形．
∴O1P2+O2P2=OP2=R2，得R2=4，
∴球O的表面积S=4πR2=16π．
故选B．
解：设两个半平面α，β截球O的两个截面圆的圆心分别为O1，02，连接O1P，O2P，OP，如图所示由球的截面圆性质及球的切线性质得OO1⊥α，OO2⊥β．OP⊥l，且O1P=1，O2P=
| 3 |
∴l⊥面OO1P，l⊥面OO2P，∴O1，02，O，P四点共面，
∠O1PO2 为二面角α-l-β的平面角，∠O1PO2=
| π |
| 2 |
∴O1P2+O2P2=OP2=R2，得R2=4，
∴球O的表面积S=4πR2=16π．
故选B．
点评：本题考查了二面角的度量，球的截面圆性质及表面积计算．本题得出O1P2+O2P2=OP2=R2是关键．
练习册系列答案
相关题目
（理）设直线l与球O有且只有一个公共点P，从直线l出发的两个半平面α，β截球O的两个截面圆的半径分别为1和
，二面角α-l-β的平面角为150°，则球O的表面积为（ ）
| 3 |
| A、4π | B、16π |
| C、28π | D、112π |
，二面角α-l-β的平面角为
，则球O的表面积为 ．