题目内容
已知偶函数f(x)x∈R满足:任意的x∈R,都有f(x+2)=f(x),且x∈[0,1]时,f(x)=x则函数F(x)=f(x)-log
的所有零点之和为
|x-4| 5 |
32
32
.分析:分别作出函数y=f(x)、y=log5|x-1|的图象,结合函数的对称性,即可求得结论.
解答:解:∵任意的x∈R,都有f(x+2)=f(x),∴函数y=f(x)的周期为2,
又当x∈[0,1]时,f(x)=x,结合函数f(x)为偶函数,
可在坐标系中作出函数f(x)的图象,
而函数y=log
的图象可由函数y=log
的图象向右平移4个单位得到,
在同一个坐标系中作图如下:
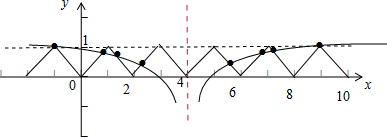
可知两函数的图象均关于x=4对称,故每对交点的和为8,
而它们共4对交点,故总和为8×4=32
故答案为:32
又当x∈[0,1]时,f(x)=x,结合函数f(x)为偶函数,
可在坐标系中作出函数f(x)的图象,
而函数y=log
|x-4| 5 |
|x| 5 |
在同一个坐标系中作图如下:

可知两函数的图象均关于x=4对称,故每对交点的和为8,
而它们共4对交点,故总和为8×4=32
故答案为:32
点评:本题考查函数的零点,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
相关题目
已知函数f(x)、g(x),下列说法正确的是( )
| A、f(x)是奇函数,g(x)是奇函数,则f(x)+g(x)是奇函数 | B、f(x)是偶函数,g(x)是偶函数,则f(x)+g(x)是偶函数 | C、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)一定是奇函数或偶函数 | D、f(x)是奇函数,g(x)是偶函数,则f(x)+g(x)可以是奇函数或偶函数 |