题目内容
在正方体的顶点中任选3个顶点连成的所有三角形中,所得的三角形是直角三角形但非等腰直角三角形的概率是 .
【答案】分析:根据题意可先求正方体的8个顶点中任选3个顶点连成的所有三角形的个数,再求出三角形是直角三角形但非等腰直角三角形的个数,代入古典概率的计算公式可求.
解答:解:正方体的8个顶点中任选3个顶点连成的所有三角形中共有C83
记“三角形是直角三角形但非等腰直角三角形“为事件A.则A包含的情况:由正方体的棱、面对角线、正方体的对角线构成的三角形符合条件共有2×12=24个
由古典概率的计算公式可得P(A)=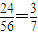
故答案为:
点评:本题主要与立体几何的常见图形:正方体结合,考查了古典概率的计算公式的应用,属于基础知识的简单运用.
解答:解:正方体的8个顶点中任选3个顶点连成的所有三角形中共有C83
记“三角形是直角三角形但非等腰直角三角形“为事件A.则A包含的情况:由正方体的棱、面对角线、正方体的对角线构成的三角形符合条件共有2×12=24个
由古典概率的计算公式可得P(A)=
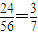
故答案为:

点评:本题主要与立体几何的常见图形:正方体结合,考查了古典概率的计算公式的应用,属于基础知识的简单运用.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
 B、
B、 C、
C、 D、
D、