题目内容
10辆货车从A站出发以时速v千米/小时,匀速驶往相距400千米的B站,为安全起见,要求每辆货车的间隔等于kv2千米(k为常数,货车长度忽略不计),
(1)将第一辆货车由A站出发到最后一辆货车到达B站所需的时间t表示成时速v的函数;
(2)若k=
,则货车的时速为多少时,(1)中所需的时间t最短?最短时间为多少?
(1)将第一辆货车由A站出发到最后一辆货车到达B站所需的时间t表示成时速v的函数;
(2)若k=
| 1 |
| 144 |
(1)最后一辆货车到达的时间包括两部分,一是两个位置相距的路程所需要的时间,二是十辆车之间的九倍的车距所用的时间,得到
t=
(v>0)…(4分)
(2)由(1)中
t=
又∵k=
,
∴t=
≥2
=10
当且仅当v=80时,取等
故当时速为80千米/小时,最短时间为10小时;
t=
| 400+9k v2 |
| v |
(2)由(1)中
t=
| 400+9k v2 |
| v |
又∵k=
| 1 |
| 144 |
∴t=
400+
| ||
| v |
|
当且仅当v=80时,取等
故当时速为80千米/小时,最短时间为10小时;

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
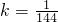 ,则货车的时速为多少时,(1)中所需的时间t最短?最短时间为多少?
,则货车的时速为多少时,(1)中所需的时间t最短?最短时间为多少?