题目内容
10辆货车从A站出发以时速v千米/小时,匀速驶往相距400千米的B站,为安全起见,要求每辆货车的间隔等于kv2千米(k为常数,货车长度忽略不计),
(1)将第一辆货车由A站出发到最后一辆货车到达B站所需的时间t表示成时速v的函数;
(2)若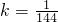 ,则货车的时速为多少时,(1)中所需的时间t最短?最短时间为多少?
,则货车的时速为多少时,(1)中所需的时间t最短?最短时间为多少?
解:(1)最后一辆货车到达的时间包括两部分,一是两个位置相距的路程所需要的时间,二是十辆车之间的九倍的车距所用的时间,得到
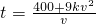 (v>0)…(4分)
(v>0)…(4分)
(2)由(1)中
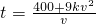
又∵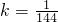 ,
,
∴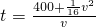
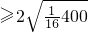 =10
=10
当且仅当v=80时,取等
故当时速为80千米/小时,最短时间为10小时;
分析:(1)最后一辆货车到达的时间包括两部分,一是两个位置相距的路程所需要的时间,二是十辆车之间的九倍的车距所用的时间,表示出两种情况所用的时间,相加得到结果.
(2)对第一问做出的结果进行整理,得到满足基本不等式的形式,利用基本不等式进行求解,得到最小值,注意等号成立的条件.
点评:本题考查的知识点是函数模型的选择与应用,基本不等式在最值问题中的应用,考查了学生对基本不等式的理解和运用.其中正确理解第一辆货车由A站出发到最后一辆货车到达B站所需的时间,并求出其表达式是解答本题的.
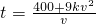 (v>0)…(4分)
(v>0)…(4分)(2)由(1)中
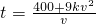
又∵
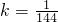 ,
,∴
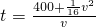
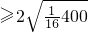 =10
=10当且仅当v=80时,取等
故当时速为80千米/小时,最短时间为10小时;
分析:(1)最后一辆货车到达的时间包括两部分,一是两个位置相距的路程所需要的时间,二是十辆车之间的九倍的车距所用的时间,表示出两种情况所用的时间,相加得到结果.
(2)对第一问做出的结果进行整理,得到满足基本不等式的形式,利用基本不等式进行求解,得到最小值,注意等号成立的条件.
点评:本题考查的知识点是函数模型的选择与应用,基本不等式在最值问题中的应用,考查了学生对基本不等式的理解和运用.其中正确理解第一辆货车由A站出发到最后一辆货车到达B站所需的时间,并求出其表达式是解答本题的.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目