题目内容
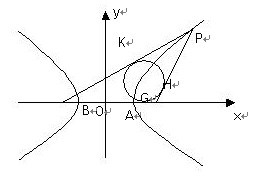
(20分)设双曲线解析:如图,记双曲线在![]() 轴上的两顶点为A(1, 0), B(-1, 0),G为
轴上的两顶点为A(1, 0), B(-1, 0),G为![]() 的内切圆在边
的内切圆在边![]() 上的切点,H为
上的切点,H为![]() 的内切圆在边
的内切圆在边![]() 上的切点,K为
上的切点,K为![]() 的内切圆在边
的内切圆在边![]() 上的切点。则有
上的切点。则有
![]()
![]()
![]() --------------------------------- 5分
--------------------------------- 5分
由双曲线的定义知,G必在双曲线上,于是G与A(1, 0)重合,是定点。
而![]() 。根据圆外一点到该圆的两切点的距离相等,所以
。根据圆外一点到该圆的两切点的距离相等,所以![]() 的内切圆在边
的内切圆在边![]() 上的切点的轨迹是以
上的切点的轨迹是以![]() 为圆心,
为圆心,![]() 为半径的圆弧。------- 10分
为半径的圆弧。------- 10分
因为![]() 是在
是在![]() 第一象限的曲线上移动,当
第一象限的曲线上移动,当![]() 沿双曲线趋于无穷时,与
沿双曲线趋于无穷时,与![]() 轴正向的交角
轴正向的交角![]() 的正切的极限是
的正切的极限是
![]()
即 ![]() 。 故点H的轨迹方程为 (极坐标形式)
。 故点H的轨迹方程为 (极坐标形式)
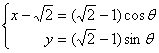 , (
, (![]() ) --------------------------------- 15分
) --------------------------------- 15分
也可以用直角坐标形式。
由于G与A(1, 0)重合,是定点,故该内切圆圆心的轨迹是直线段,方程为
![]() (
(![]() )。 -------------------------------- 20分
)。 -------------------------------- 20分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
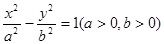 的左、右焦点分别为
的左、右焦点分别为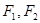 ,离心率为
,离心率为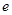 ,过
,过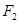 的直线与双曲线的右支交于
的直线与双曲线的右支交于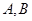 两点,若
两点,若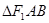 是以
是以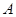 为直角顶点的等腰直角三角形,则
为直角顶点的等腰直角三角形,则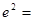 _______.
_______.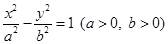 的左、右焦点分别为
的左、右焦点分别为 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,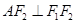 ,原点
,原点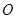 到直线
到直线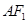 的距离为
的距离为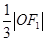 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)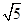 或
或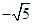 (B)
(B)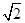 或
或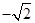 (C)1或
(C)1或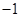 (D)
(D)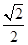 或
或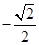
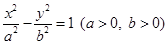 的左、右焦点分别为
的左、右焦点分别为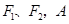 是双曲线渐近线上的一点,
是双曲线渐近线上的一点,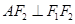 ,原点
,原点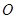 到直线
到直线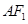 的距离为
的距离为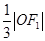 ,则渐近线的斜率为 (
)
,则渐近线的斜率为 (
)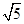 或
或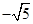 (B)
(B)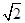 或
或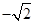 (C)1或
(C)1或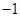 (D)
(D)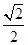 或
或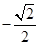
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,过点
,过点 、
、 .若△
.若△ 为正三角形,则该双曲线的离心率为
为正三角形,则该双曲线的离心率为
 B.
B. C.
C. D.
D.