题目内容
对于下列命题:①在△ABC中,若sin2A=sin2B,则△ABC为等腰三角形;
②已知a,b,c是△ABC的三边长,若a=2,b=5,
 ,则△ABC有两组解;
,则△ABC有两组解;③设
 ,
, ,
,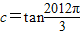 ,则a>b>c;
,则a>b>c;④将函数
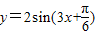 图象向左平移
图象向左平移 个单位,得到函数
个单位,得到函数 图象.
图象.其中正确命题的序号是 .
【答案】分析:①由于sin2A=sin2B,则2A=2B,或2A+2B=π,可以得到以△ABC为等腰三角形或直角三角形;
②由正弦定理可求出sinB的值,进而判断②的正误;
③依据三角函数的诱导公式求出a,b,c的值,进而得到命题正误;
④依据图象左加右减的原则,再由诱导公式,可判断命题的真假.
解答:解:①、由于sin2A=sin2B,则2A=2B,或2A+2B=π,∴A=B,或A+B=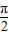 ,所以△ABC为等腰三角形或直角三角形,故此命题错;
,所以△ABC为等腰三角形或直角三角形,故此命题错;
②、由正弦定理知,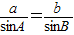 ,∴
,∴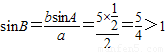 ,显然无解,故此命题错;
,显然无解,故此命题错;
③、∵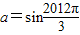 =
= ,
,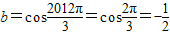 ,
,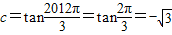 ,∴a>b>c,此命题正确;
,∴a>b>c,此命题正确;
④、由于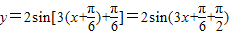 =
=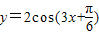 ,所以此命题正确.
,所以此命题正确.
故答案为 ③④.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了正弦定理和三角函数的一些性质,我们要对四个结论逐一进行判断,可以得到正确的结论.
②由正弦定理可求出sinB的值,进而判断②的正误;
③依据三角函数的诱导公式求出a,b,c的值,进而得到命题正误;
④依据图象左加右减的原则,再由诱导公式,可判断命题的真假.
解答:解:①、由于sin2A=sin2B,则2A=2B,或2A+2B=π,∴A=B,或A+B=
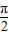 ,所以△ABC为等腰三角形或直角三角形,故此命题错;
,所以△ABC为等腰三角形或直角三角形,故此命题错;②、由正弦定理知,
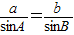 ,∴
,∴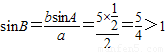 ,显然无解,故此命题错;
,显然无解,故此命题错;③、∵
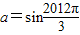 =
= ,
,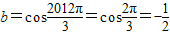 ,
,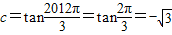 ,∴a>b>c,此命题正确;
,∴a>b>c,此命题正确;④、由于
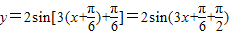 =
=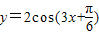 ,所以此命题正确.
,所以此命题正确.故答案为 ③④.
点评:本题考查的知识点是,判断命题真假,比较综合的考查了正弦定理和三角函数的一些性质,我们要对四个结论逐一进行判断,可以得到正确的结论.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 (
( 为常数,且
为常数,且 ),对于下列命题:
),对于下列命题: 在每一点处都连续;
在每一点处都连续; ,则函数
,则函数 处可导;
处可导; ;
; ,恒有
,恒有 .
.
 (
( 为常数,且
为常数,且 ),对于下列命题:
),对于下列命题: 在每一点处都连续;
在每一点处都连续; ,则函数
,则函数 处可导;
处可导; ;
; ,恒有
,恒有 .
.