题目内容
已知:集合M是满足下列性质的函数f(x)的全体:在定义域内存在x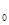 ,使得
,使得
f(x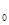 +1)=f(x
+1)=f(x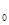 )+f(1)成立。
)+f(1)成立。
(1)函数f(x)=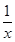 是否属于集合M?说明理由;
是否属于集合M?说明理由;
(2)设函数f(x)=lg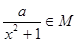 ,求实数a的取值范围;
,求实数a的取值范围;
(3)证明:函数f(x)=2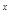 +x
+x
 M。
M。
【答案】
解:(Ⅰ)f(x)=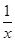 的定义域为
的定义域为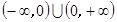 ,
,
令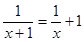 ,整理得x
,整理得x +x+1=0,△=-3<0,
+x+1=0,△=-3<0,
因此,不存在x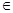
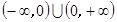 使得f(x+1)=f(x)+f(1)成立,所以f(x)=
使得f(x+1)=f(x)+f(1)成立,所以f(x)=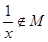 ; 3分
; 3分
(Ⅱ)f(x)=lg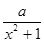 的定义域为R,f(1)=lg
的定义域为R,f(1)=lg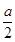 ,a>0,
,a>0,
若f(x)= lg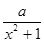
 M,则存在x
M,则存在x R使得lg
R使得lg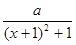 =lg
=lg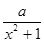 +lg
+lg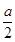 ,
,
整理得存在x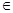 R使得(a
R使得(a -2a)x
-2a)x +2a
+2a x+(2a
x+(2a -2a)=0.
-2a)=0.
(1)若a -2a=0即a=2时,方程化为8x+4=0,解得x=-
-2a=0即a=2时,方程化为8x+4=0,解得x=-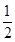 ,满足条件:
,满足条件:
(2)若a -2a
-2a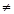 0即a
0即a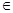
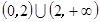 时,令△≥0,解得a
时,令△≥0,解得a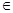
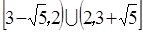 ,综上,a
,综上,a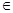 [3-
[3-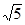 ,3+
,3+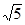 ];
7分
];
7分
(Ⅲ)f(x)=2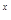 +x
+x 的定义域为R,
的定义域为R,
令2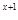 +(x+1)
+(x+1) =(2
=(2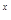 +x
+x )+(2+1),整理得2
)+(2+1),整理得2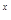 +2x-2=0,
+2x-2=0,
令g(x)=2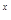 +2x-2,所以g(0)·g(1)=-2<0,
+2x-2,所以g(0)·g(1)=-2<0,
即存在x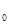
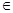 (0,1)使得g(x)=2
(0,1)使得g(x)=2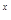 +2x-2=0,
+2x-2=0,
亦即存在x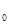
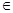 R使得2
R使得2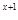 +(x+1)
+(x+1) =(2
=(2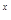 +x
+x )+(2+1),故f(x)=2
)+(2+1),故f(x)=2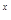 +x
+x
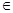 M。 10分
M。 10分
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目