题目内容
18、18、三个女生和五个男生排成一排．
（1）如果女生必须全排在一起，有多少种不同的排法？
（2）如果女生必须全分开，有多少种不同的排法？
（3）如果两端都不能排女生，有多少种不同的排法？
（4）如果两端不能都排女生，有多少种不同的排法？
（1）如果女生必须全排在一起，有多少种不同的排法？
（2）如果女生必须全分开，有多少种不同的排法？
（3）如果两端都不能排女生，有多少种不同的排法？
（4）如果两端不能都排女生，有多少种不同的排法？
分析：对于（1）（2）都比较简单可以概率的求法直接作答．对于（3）因为两端都不能排女生，所以两端只能从5个男生中选2个排在两端，故可先把两端的2个男生排好，在排其他的即可作答．对于（4）对两端不能都排女生的情况可以求其反面的情况，在用总共的排法减去两端都是女生的排法即可得到答案．
解答：解：（1）女生全部排在一起有P66P33=4320种．
（2）女生必须全分开有P55P63=14400种．
（3）因为两端都不能排女生，所以两端只能从5个男生中选2个排在两端，有P52种排法，其余6人有P66种排法，
所以共有P52•P66=14400种排法．
（4）8个人站成一排共有P88种不同的排法，排除掉两端都是女生的排法有P25•P66种，
所以符合条件的排法有P88-P52•P66=36000种．
（2）女生必须全分开有P55P63=14400种．
（3）因为两端都不能排女生，所以两端只能从5个男生中选2个排在两端，有P52种排法，其余6人有P66种排法，
所以共有P52•P66=14400种排法．
（4）8个人站成一排共有P88种不同的排法，排除掉两端都是女生的排法有P25•P66种，
所以符合条件的排法有P88-P52•P66=36000种．
点评：此题主要考查排列组合及简单计数问题，在做此类题目的时候必须要仔细分析题目的条件加以分析再作答即可得到结果，属于中等难度的题目．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
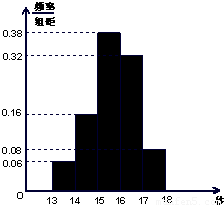
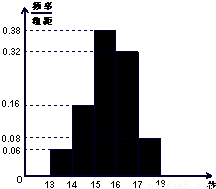
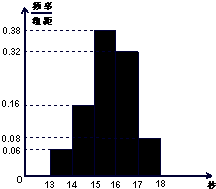（2012•珠海二模）某学校900名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
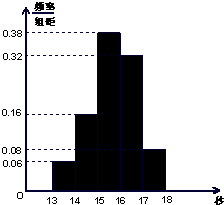（2012•珠海二模）某学校900名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组[13，14），第二组[14，15），…，第五组[17，18]，如图是按上述分组方法得到的频率分布直方图．
