题目内容
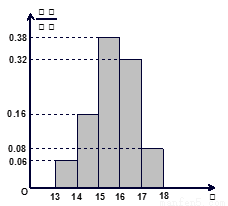
某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计本年级900名学生中,成绩属于第三组的人数;
(3)若样本第一组中只有一个女生,其他都是男生,第五组则只有一个男生,其他都是女生,现从第一、五组中各抽一个同学组成一个新的组,求这个新组恰好由一个男生和一个女生构成的概率.
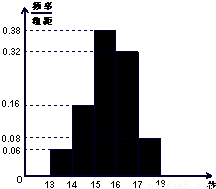
【答案】分析:(1)根据题意,成绩在第一组的为优秀,其频率为0.06,由频率计算公式即可算出该样本中成绩优秀的人数;
(2)由频率分布直方图知成绩在第三组的频率0.38,因此估计成绩属于第三组的人数约为900×0.38=342人;
(3)由频率计算公式得样本中第一组共有3人,得第五组共有4人.因此记第一组三人记为1、2、3,其中1、2为男生,3为女生;第五组四人记为a、b、c、d.其中a为男生,b、c、d为女生.用列表格的方法计算出基本事件的总数共有12个,而新组恰好由一个男生和一个女生构成的基本事件有7个.由此结合古典概型计算公式即可算出所求概率.
解答:解:(1)由频率分布直方图知,成绩在第一组的为优秀,频率为0.06,
结合样本容量等于50,可得优秀人数为:50×0.06=3
∴该样本中成绩优秀的人数为3. …(3分)
(2)由频率分布直方图知,成绩在第三组的频率0.38,以此估计本年级900名学生成绩属于第三组的概率为0.38,
从而可得成绩属于第三组的人数的估计值为:900×0.38=342
∴估计本年级900名学生中,成绩属于第三组的人数为342.…(7分)
(3)样本中第一组共有3人,
由第五组的频率为0.08,可得第五组共有4人.
其中第五组四人记为a、b、c、d.其中a为男生,b、c、d为女生,
第一组三人记为1、2、3,其中1、2为男生,3为女生.
基本事件列表如下:
可得基本事件总共有12个 …(10分)
恰为一男一女的事件有1b,1c,1d,2b,2c,2d,3a;共7个 …(12分)
∴新组恰由一男一女构成的概率是P=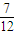 .…(13分)
.…(13分)
点评:本题给出频率分布直方图,求样本中成绩优秀的人数、900名学生中成绩属于第三组的人数的估计值,并求一个随机事件的概率.着重考查了频率分布的计算公式和古典概型计算公式等知识,属于基础题.
(2)由频率分布直方图知成绩在第三组的频率0.38,因此估计成绩属于第三组的人数约为900×0.38=342人;
(3)由频率计算公式得样本中第一组共有3人,得第五组共有4人.因此记第一组三人记为1、2、3,其中1、2为男生,3为女生;第五组四人记为a、b、c、d.其中a为男生,b、c、d为女生.用列表格的方法计算出基本事件的总数共有12个,而新组恰好由一个男生和一个女生构成的基本事件有7个.由此结合古典概型计算公式即可算出所求概率.
解答:解:(1)由频率分布直方图知,成绩在第一组的为优秀,频率为0.06,
结合样本容量等于50,可得优秀人数为:50×0.06=3
∴该样本中成绩优秀的人数为3. …(3分)
(2)由频率分布直方图知,成绩在第三组的频率0.38,以此估计本年级900名学生成绩属于第三组的概率为0.38,
从而可得成绩属于第三组的人数的估计值为:900×0.38=342
∴估计本年级900名学生中,成绩属于第三组的人数为342.…(7分)
(3)样本中第一组共有3人,
由第五组的频率为0.08,可得第五组共有4人.
其中第五组四人记为a、b、c、d.其中a为男生,b、c、d为女生,
第一组三人记为1、2、3,其中1、2为男生,3为女生.
基本事件列表如下:
| a | b | c | d | |
| 1 | 1a | 1b | 1c | 1d |
| 2 | 2a | 2b | 2c | 2d |
| 3 | 3a | 3b | 3c | 3d |
恰为一男一女的事件有1b,1c,1d,2b,2c,2d,3a;共7个 …(12分)
∴新组恰由一男一女构成的概率是P=
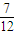 .…(13分)
.…(13分)点评:本题给出频率分布直方图,求样本中成绩优秀的人数、900名学生中成绩属于第三组的人数的估计值,并求一个随机事件的概率.着重考查了频率分布的计算公式和古典概型计算公式等知识,属于基础题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.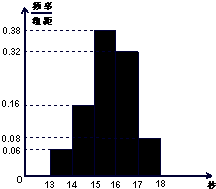 (2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.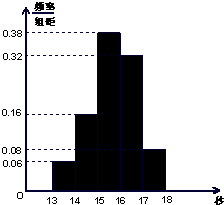 (2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
(2012•珠海二模)某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.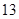 秒与
秒与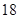 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组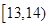 ,第二组
,第二组 ,…,第五组
,…,第五组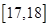 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.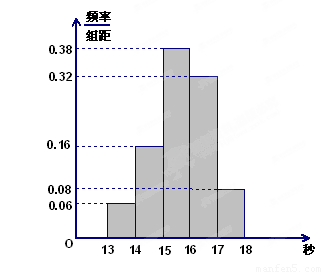
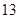 秒与
秒与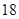 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组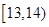 ,第二组
,第二组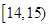 ,…,第五组
,…,第五组 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.