题目内容
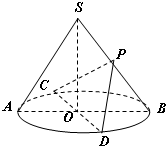 如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.
如图,圆锥SO中,AB、CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点.(1)求证:SA∥平面PCD;
(2)求异面直线SA与PD所成角的正切值.
分析:(1)根据OP为△ABS的中位线,故有SA∥OP.再根据直线和平面平行的判定定理证得SA∥平面PCD.
(2)由(1)结合异面直线所成的角的定义可得∠OPD即为异面直线SA与PD所成角.直角三角形OPD中,根据tan∠OPD=
,运算求得结果.
(2)由(1)结合异面直线所成的角的定义可得∠OPD即为异面直线SA与PD所成角.直角三角形OPD中,根据tan∠OPD=
| OD |
| OP |
解答: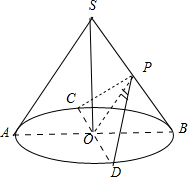 解:(1)圆锥SO中,P为SB的中点,故OP为△ABS的中位线,故有SA∥OP.
解:(1)圆锥SO中,P为SB的中点,故OP为△ABS的中位线,故有SA∥OP.
由于OP在平面PCD内,而SA不在平面PCD内,故有SA∥平面PCD.
(2)由SA∥OP,结合异面直线所成的角的定义可得∠OPD即为异面直线SA与PD所成角.
由AB、CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,可得CD⊥平面SOB,
而OP在平面SOB内,故有CD⊥OP.
直角三角形OPD中,OD=2,OP=
SA=
SB=
,故tan∠OPD=
=
=
,
即异面直线SA与PD所成角的正切值为
.
 解:(1)圆锥SO中,P为SB的中点,故OP为△ABS的中位线,故有SA∥OP.
解:(1)圆锥SO中,P为SB的中点,故OP为△ABS的中位线,故有SA∥OP.由于OP在平面PCD内,而SA不在平面PCD内,故有SA∥平面PCD.
(2)由SA∥OP,结合异面直线所成的角的定义可得∠OPD即为异面直线SA与PD所成角.
由AB、CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,可得CD⊥平面SOB,
而OP在平面SOB内,故有CD⊥OP.
直角三角形OPD中,OD=2,OP=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| OD |
| OP |
| 2 | ||
|
| 2 |
即异面直线SA与PD所成角的正切值为
| 2 |
点评:本题主要考查直线和平面平行的判定定理的应用,异面直线所成的角的定义和求法,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
