题目内容
设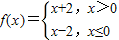 ,则不等式f(x)<x2的解集是( )
,则不等式f(x)<x2的解集是( )A.(2,+∞)∪(-∞,0]
B.R
C.[0,2)
D.(-∞,0)
【答案】分析:根据所给的分段函数,当x小于等于0和x大于0两种情况,根据分段函数分别得到f(x)的解析式,把得到的f(x)的解析式分别代入不等式得到两个一元二次不等式,分别求出解集,求出两解集的并集即可得到原不等式的解集.
解答:解:当x>0时,f(x)=x+2,代入不等式得:x+2<x2,
即(x-2)(x+1)>0,解得x>2,x<-1,所以原不等式的解集为(2,+∞);
当x≤0时,f(x)=x-2,代入不等式得:x-2<x2,
解得x∈R,所以原不等式的解集为(-∞,0],
综上原不等式的解集为(2,+∞)∪(-∞,0].
故选A
点评:本题考查了不等式的解法及分段函数,考查分类讨论的思想,本题解题的关键是对于求出的范围一定要和分段函数的范围分别并起来,本是一个基础题.
解答:解:当x>0时,f(x)=x+2,代入不等式得:x+2<x2,
即(x-2)(x+1)>0,解得x>2,x<-1,所以原不等式的解集为(2,+∞);
当x≤0时,f(x)=x-2,代入不等式得:x-2<x2,
解得x∈R,所以原不等式的解集为(-∞,0],
综上原不等式的解集为(2,+∞)∪(-∞,0].
故选A
点评:本题考查了不等式的解法及分段函数,考查分类讨论的思想,本题解题的关键是对于求出的范围一定要和分段函数的范围分别并起来,本是一个基础题.

练习册系列答案
相关题目
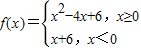 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )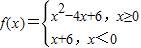 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )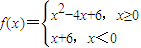 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )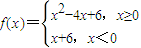 则不等式f(x)>f(1)的解集是( )
则不等式f(x)>f(1)的解集是( )