题目内容
设曲线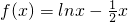 在点
在点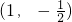 处的切线与直线ax-y+1=0垂直,则a=
处的切线与直线ax-y+1=0垂直,则a=
- A.2
- B.

- C.-2
- D.

C
分析:由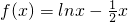 ,知
,知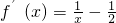 ,故曲线
,故曲线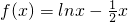 在点
在点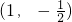 处的切线的斜率k=
处的切线的斜率k=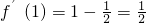 ,由曲线
,由曲线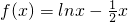 在点
在点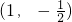 处的切线与直线ax-y+1=0垂直,能求出a的值.
处的切线与直线ax-y+1=0垂直,能求出a的值.
解答:∵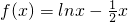 ,
,
∴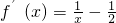 ,
,
∴曲线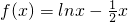 在点
在点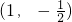 处的切线的斜率k=
处的切线的斜率k=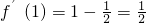 ,
,
∵曲线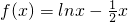 在点
在点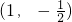 处的切线与直线ax-y+1=0垂直,
处的切线与直线ax-y+1=0垂直,
∴直线ax-y+1=0的斜率k′=a=-2.
故选C.
点评:本题考查导数的几何意义的求法,是基础题.解题时要认真审题,仔细解答,注意直线与直线垂直的性质的灵活运用.
分析:由
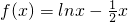 ,知
,知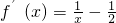 ,故曲线
,故曲线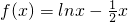 在点
在点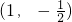 处的切线的斜率k=
处的切线的斜率k=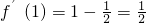 ,由曲线
,由曲线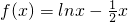 在点
在点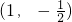 处的切线与直线ax-y+1=0垂直,能求出a的值.
处的切线与直线ax-y+1=0垂直,能求出a的值.解答:∵
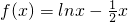 ,
,∴
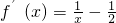 ,
,∴曲线
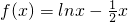 在点
在点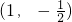 处的切线的斜率k=
处的切线的斜率k=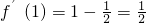 ,
,∵曲线
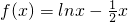 在点
在点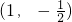 处的切线与直线ax-y+1=0垂直,
处的切线与直线ax-y+1=0垂直,∴直线ax-y+1=0的斜率k′=a=-2.
故选C.
点评:本题考查导数的几何意义的求法,是基础题.解题时要认真审题,仔细解答,注意直线与直线垂直的性质的灵活运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数. 表示
表示 ;
; ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 ,求
,求 在点
在点 处的切线与直线
处的切线与直线 垂直,则
垂直,则 .
. 在点
在点 处的切线与直线
处的切线与直线 平行,则实数
平行,则实数 等于( )
等于( ) B.
B. C.
C. D.
D.
 在点
在点 处的切线与
处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,则
,则 的值为 。
的值为 。