题目内容
已知双曲线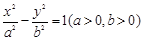 ,
,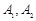 为实轴顶点,
为实轴顶点,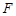 是右焦点,
是右焦点,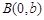 是虚轴端点,
是虚轴端点,
若在线段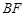 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点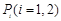 ,使得
,使得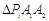 构成以
构成以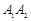 为斜边的
为斜边的
直角三角形,则双曲线离心率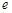 的取值范围是( )
的取值范围是( )
A.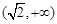 | B.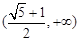 | C.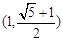 | D.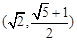 |
D
解析试题分析:由题意知,要使得在线段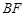 上(不含端点)存在不同的两点
上(不含端点)存在不同的两点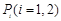 ,使得
,使得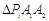 构成以
构成以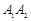 为斜边的直角三角形,只需以
为斜边的直角三角形,只需以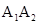 为直径的圆与线段
为直径的圆与线段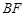 相交于两点,且端点不是交点即可,故圆心
相交于两点,且端点不是交点即可,故圆心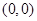 到直线
到直线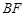 的距离
的距离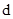 满足
满足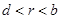 ,即
,即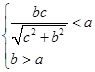 ,解得
,解得 ,故
,故
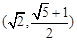
考点:1、双曲线的简单几何性质;2、直线和圆的位置关系.

练习册系列答案
相关题目
设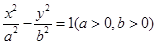 的离心率为
的离心率为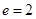 ,则
,则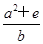 的最小值为( )
的最小值为( )
A.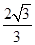 | B.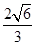 | C.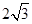 | D.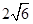 |
已知双曲线 与椭圆
与椭圆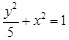 有相同的焦点,则该双曲线的渐近线方程为( )
有相同的焦点,则该双曲线的渐近线方程为( )
A. | B. | C. | D. |
双曲线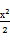 -
-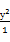 =1的焦点坐标是( )
=1的焦点坐标是( )
| A.(1,0), (-1,0) | B.(0,1),(0,-1) |
C.(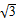 ,0),(- ,0),(-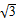 ,0) ,0) | D.(0,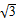 ),(0,- ),(0,-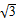 ) ) |
设抛物线的顶点在原点,准线方程为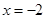 ,则抛物线的方程是( )
,则抛物线的方程是( )
A.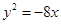 | B.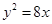 | C.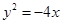 | D.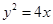 |
已知椭圆C的方程为 (m>0),如果直线y=
(m>0),如果直线y=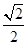 x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m的值为( )
| A.2 | B.2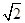 |
| C.8 | D.2 |
椭圆 =1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
=1的焦点为F1和F2,点P在椭圆上,如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
| A.7倍 | B.5倍 | C.4倍 | D.3倍 |
已知点F是双曲线 的左焦点,点E是该双曲线的右焦点,过点F且垂直于x轴的
的左焦点,点E是该双曲线的右焦点,过点F且垂直于x轴的
直线与双曲线交于A,B两点,△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( )
| A.(1,+∞) | B.(1,2) |
C. | D. |

