题目内容
设f(| x |
| 1 |
| x |
| x |
(1)求f(x)的表达式.
(2)设函数g(x)=aχ-
| 1 |
| x2 |
(3)解不等式f(x)-χ>2.
分析:(1)把已知解析式中的
设为t,解出x后代入即可确定出f(x)的解析式;
(2)把求出的f(x)的解析式代入到g(x)中确定出g(x)的解析式,求出g(x)的定义域,求出g(1)的值,由于g(-1)不存在,进而不存在实数a使得g(x)为奇函数;
(3)把f(x)的解析式代入到不等式中,因式分解后,根据x大于0和图形即可得到原不等式的解集.
| x |
(2)把求出的f(x)的解析式代入到g(x)中确定出g(x)的解析式,求出g(x)的定义域,求出g(1)的值,由于g(-1)不存在,进而不存在实数a使得g(x)为奇函数;
(3)把f(x)的解析式代入到不等式中,因式分解后,根据x大于0和图形即可得到原不等式的解集.
解答:解:(1)由f(
)=
+2
,设
=t,解得x=t2(t>0),
把x=t2代入得:f(t)=
+2t,即f(x)=
+2x(x>0);
(2)∵g(x)=ax2-
+f(x)=ax2+2x,定义域为(0,+∞),
∵g(1)=2+a,而g(-1)不存在,
∴g(1)≠-g(-1),即不存在实数a使得g(x)为奇函数;
(3)∵f(x)-x>2,即
+x-2>0,
去分母得:x3-2x2+1>0,即(x3-x2)-(x2-1)>0,
因式分解得:(x-1)(x2-x-1)>0,
即(x-1)(x-
)(x-
)>0,
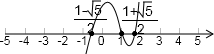
∴结合x>0和图形得:0<x<1或x>
.
因此原不等式的解集为{x|0<x<1或x>
}.
| x |
| 1 |
| x |
| x |
| x |
把x=t2代入得:f(t)=
| 1 |
| t2 |
| 1 |
| x2 |
(2)∵g(x)=ax2-
| 1 |
| x2 |
∵g(1)=2+a,而g(-1)不存在,
∴g(1)≠-g(-1),即不存在实数a使得g(x)为奇函数;
(3)∵f(x)-x>2,即
| 1 |
| x2 |
去分母得:x3-2x2+1>0,即(x3-x2)-(x2-1)>0,
因式分解得:(x-1)(x2-x-1)>0,
即(x-1)(x-
1+
| ||
| 2 |
1-
| ||
| 2 |

∴结合x>0和图形得:0<x<1或x>
1+
| ||
| 2 |
因此原不等式的解集为{x|0<x<1或x>
| ||
| 2 |
点评:此题考查学生掌握函数解析式的求法及奇函数的性质,考查了数形结合的数学思想的运用,是一道中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目