题目内容
13.设函数f(x)=|x-a|+1,a∈R(1)当a=4时,解不等式f(x)<1+|2x+1|
(2)若f(x)≤2的解集为[0,2],$\frac{1}{m}$+$\frac{1}{n}$=a(m>0,n>0)求证:m+2n≥3+2$\sqrt{2}$.
分析 对第(1)问,将a=3代入函数的解析式中,利用分段讨论法解绝对值不等式即可;
对第(2)问,先由已知解集{x|0≤x≤2}确定a值,再将“m+2n”改写为“(m+2n)($\frac{1}{m}$+$\frac{1}{n}$)”,展开后利用基本不等式可完成证明.
解答 (1)解:当a=4时,不等式f(x)<1+|2x+1|即为|x-4|<|2x+1|
|①当x≥4时,原不等式化为x-4<2x+1,得x>-5,故x≥4;
②当-$\frac{1}{2}$≤x<4时,原不等式化为4-x<2x+1,得x>1,故1<x<4;
③当x<-$\frac{1}{2}$时,原不等式化为4-x<-2x-1,得x<-5,故x<-5.
综合①、②、③知,原不等式的解集为(-∞,-5)∪(1,+∞);
(2)证明:由f(x)≤2得|x-a|≤1,从而-1+a≤x≤1+a,
∵f(x)≤1的解集为{x|0≤x≤2},
∴$\left\{\begin{array}{l}{-1+a=0}\\{1+a=2}\end{array}\right.$得a=1,∴$\frac{1}{m}$+$\frac{1}{n}$═a=1.
又m>0,n>0,
∴m+2n=(m+2n)($\frac{1}{m}$+$\frac{1}{n}$=)=3+($\frac{2n}{m}$+$\frac{m}{n}$)≥3+2$\sqrt{2}$,
当且仅当m=1+$\sqrt{2}$,n=1+$\frac{\sqrt{2}}{2}$时,取等号,故m+2n≥3+2$\sqrt{2}$,得证
点评 1.已知不等式的解集求参数的值,求解的一般思路是:先将原不等式求解一遍,再把结果与已知解集对比即可获得参数的值.
2.本题中,“1”的替换很关键,这是解决此类题型的一种常用技巧,应注意体会证明过程的巧妙性.


| A. | 30 | B. | 50 | C. | 60 | D. | 70 |
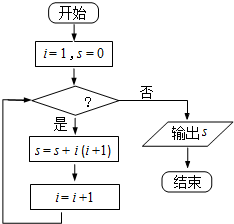
| A. | i≤5 | B. | i<5 | C. | i>5 | D. | i≥5 |
 如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )
如图,在正方形ABCD中,E、F分别是BC、CD的中点,沿AE、AF、EF把正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,P点在△AEF内的射影为O.则下列说法正确的是( )| A. | O是△AEF的垂心 | B. | O是△AEF的内心 | C. | O是△AEF的外心 | D. | O是△AEF的重心 |