题目内容
已知方程x2+4x+3=0的两个根为tan(α-β),tanβ.
(1)求tanα的值.
(2)求
的值.
(1)求tanα的值.
(2)求
| 3cosα+sinα | cosα-sinα |
分析:(1)α=(α-β)+β,利用两角和的正切公式即可求得tanα的值;
(2)将
中的弦化切即可.
(2)将
|
解答:解:(1)∵α=(α-β)+β,
∴
,
∴tanα=tan[(α-β)+β]=
=
=2.
(2)
=
=
=-5.
∴
|
∴tanα=tan[(α-β)+β]=
|
| -4 |
| 1-3 |
(2)
|
| 3+tanα |
| 1-tanα |
| 3+2 |
| 1-2 |
点评:本题考查两角和与差的正切函数,考查“弦”化“切”,考查转化思想与运算能力,属于中档题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
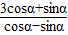 的值.
的值.