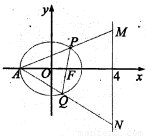
题目内容
已知椭圆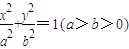 的左顶点为A,左、右焦点分别为F1,F2,且圆C:
的左顶点为A,左、右焦点分别为F1,F2,且圆C: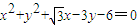 过A,F2两点.
过A,F2两点.(1)求椭圆标准的方程;
(2)设直线PF2的倾斜角为α,直线PF1的倾斜角为β,当β-α=
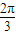 时,证明:点P在一定圆上;
时,证明:点P在一定圆上;(3)设椭圆的上顶点为Q,证明:PQ=PF1+PF2.
【答案】分析:(1)由圆C: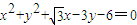 确定A,F2两点的坐标,即可求得椭圆方程;
确定A,F2两点的坐标,即可求得椭圆方程;
(2)设点P(x,y),因为F1(-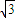 ,0),F2(
,0),F2(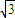 ,0),则可求
,0),则可求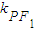 ,
,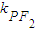 ,利用β-α=
,利用β-α=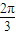 ,及差角的正切公式,即可证得结论;
,及差角的正切公式,即可证得结论;
(3)利用两点间的距离公式,计算|PQ|2=12-4y,计算出(|PF1|+|PF2|)2,即可得到结论.
解答:(1)解:圆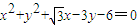 与x轴交点坐标为
与x轴交点坐标为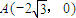 ,
,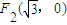 ,
,
故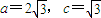 ,所以b=3,
,所以b=3,
∴椭圆方程是: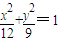 .
.
(2)证明:设点P(x,y),因为F1(-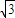 ,0),F2(
,0),F2(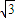 ,0),则
,0),则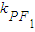 =tanβ=
=tanβ=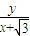 ,
,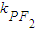 =tanα=
=tanα=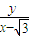 ,
,
因为β-α=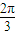 ,所以tan(β-α)=-
,所以tan(β-α)=-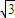 .
.
因为tan(β-α)=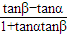 =
=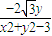 ,所以
,所以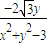 =-
=-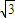 .
.
化简得x2+y2-2y=3.
所以点P在定圆x2+y2-2y=3上.
(3)证明:∵|PQ|2=x2+(y-3)2=x2+y2-6y+9,x2+y2=3+2y,∴|PQ|2=12-4y.
又|PF1|2=(x+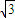 )2+y2=2y+6+2
)2+y2=2y+6+2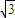 x,|PF2|2=(x-
x,|PF2|2=(x-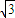 )2+y2=2y+6-2
)2+y2=2y+6-2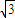 x,
x,
∴2|PF1|×|PF2|=2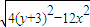 =4
=4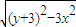 ,
,
因为3x2=9-3y2+6y,所以2|PF1|×|PF2|=4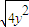 ,
,
∵β=α+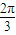 >
>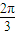 ,又点P在定圆x2+y2-2y=3上,∴y<0,
,又点P在定圆x2+y2-2y=3上,∴y<0,
所以2|PF1|×|PF2|=-8y,
从而(|PF1|+|PF2|)2=|PF1|2+2|PF1|×|PF2|+|PF2|2=4y+12-8y=12-4y=|PQ|2.
所以|PQ|=|PF1|+|PF2|.
点评:本题考查椭圆的标准方程,考查差角的正切公式,考查距离公式,考查学生分析解决问题的能力,属于中档题.
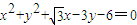 确定A,F2两点的坐标,即可求得椭圆方程;
确定A,F2两点的坐标,即可求得椭圆方程;(2)设点P(x,y),因为F1(-
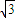 ,0),F2(
,0),F2(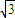 ,0),则可求
,0),则可求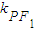 ,
,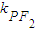 ,利用β-α=
,利用β-α=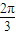 ,及差角的正切公式,即可证得结论;
,及差角的正切公式,即可证得结论;(3)利用两点间的距离公式,计算|PQ|2=12-4y,计算出(|PF1|+|PF2|)2,即可得到结论.
解答:(1)解:圆
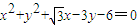 与x轴交点坐标为
与x轴交点坐标为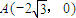 ,
,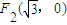 ,
,故
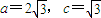 ,所以b=3,
,所以b=3,∴椭圆方程是:
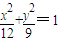 .
.(2)证明:设点P(x,y),因为F1(-
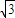 ,0),F2(
,0),F2(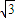 ,0),则
,0),则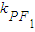 =tanβ=
=tanβ=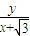 ,
,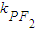 =tanα=
=tanα=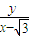 ,
,因为β-α=
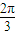 ,所以tan(β-α)=-
,所以tan(β-α)=-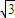 .
.因为tan(β-α)=
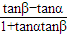 =
=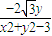 ,所以
,所以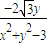 =-
=-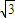 .
.化简得x2+y2-2y=3.
所以点P在定圆x2+y2-2y=3上.
(3)证明:∵|PQ|2=x2+(y-3)2=x2+y2-6y+9,x2+y2=3+2y,∴|PQ|2=12-4y.
又|PF1|2=(x+
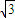 )2+y2=2y+6+2
)2+y2=2y+6+2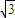 x,|PF2|2=(x-
x,|PF2|2=(x-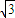 )2+y2=2y+6-2
)2+y2=2y+6-2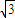 x,
x,∴2|PF1|×|PF2|=2
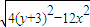 =4
=4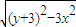 ,
,因为3x2=9-3y2+6y,所以2|PF1|×|PF2|=4
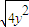 ,
,∵β=α+
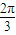 >
>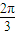 ,又点P在定圆x2+y2-2y=3上,∴y<0,
,又点P在定圆x2+y2-2y=3上,∴y<0,所以2|PF1|×|PF2|=-8y,
从而(|PF1|+|PF2|)2=|PF1|2+2|PF1|×|PF2|+|PF2|2=4y+12-8y=12-4y=|PQ|2.
所以|PQ|=|PF1|+|PF2|.
点评:本题考查椭圆的标准方程,考查差角的正切公式,考查距离公式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
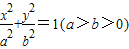 的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若
的左顶点为A,上顶点为B,右焦点为F.设线段AB的中点为M,若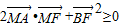 ,则该椭圆离心率的取值范围为 .
,则该椭圆离心率的取值范围为 .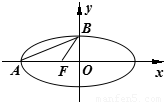 如图,已知椭圆
如图,已知椭圆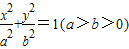 的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .
的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 . 如图,已知椭圆
如图,已知椭圆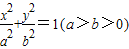 的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .
的左顶点为A,左焦点为F,上顶点为B,若∠BAO+∠BFO=90°,则该椭圆的离心率是 .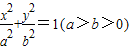 的左顶点为A,左、右焦点分别为F1,F2,且圆C:
的左顶点为A,左、右焦点分别为F1,F2,且圆C: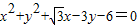 过A,F2两点.
过A,F2两点.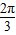 时,证明:点P在一定圆上;
时,证明:点P在一定圆上;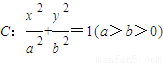 的左顶点为A,右焦点为F,且过点(1,
的左顶点为A,右焦点为F,且过点(1, ),椭圆C的焦点与曲线
),椭圆C的焦点与曲线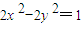 的焦点重合.
的焦点重合.