题目内容
 已知以原点
已知以原点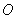 为中心,
为中心,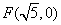 为右焦点的双曲线
为右焦点的双曲线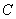 的离心率
的离心率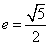 .
.
(Ⅰ)求双曲线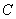 的标准方程及其渐近线方程;
的标准方程及其渐近线方程;
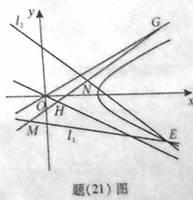
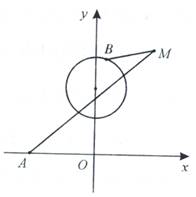
(Ⅱ)如题(21)图,已知过点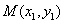 的直线
的直线 :
:
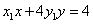 与过点
与过点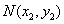 (其中
(其中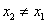 )的直线
)的直线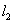 :
: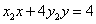 的交点
的交点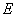 在双曲线
在双曲线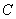 上,直线
上,直线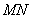 与双曲线的两条渐近线分别交于
与双曲线的两条渐近线分别交于 、
、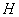 两点,求
两点,求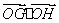 的值.
的值.
【答案】
 解:(I)设C的标准方程是
解:(I)设C的标准方程是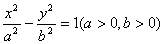 ,
,
则由题意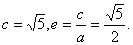
因此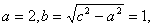
C的标准方程为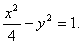
C的渐近线方程为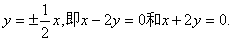
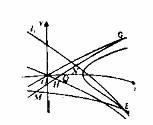
(II)解法一:如图(21)图,由题意点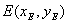 在直线
在直线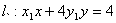 和
和
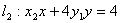 上,因此有
上,因此有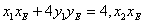
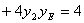
故点M、N均在直线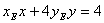 上,因此直线MN的方程为
上,因此直线MN的方程为
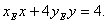
设G、H分别是直线MN与渐近线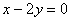 及
及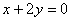 的交点,
的交点,
由方程组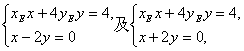
解得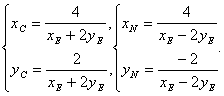
故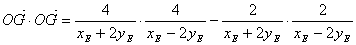
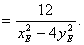
因为点E在双曲线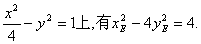
所以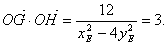
解法二:设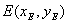 ,由方程组得
,由方程组得
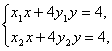
解得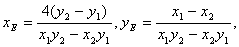
故直线MN的方程为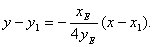
注意到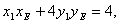 因此直线MN的方程为
因此直线MN的方程为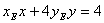 ,
,
下同解法一.

练习册系列答案
相关题目
 已知以原点
已知以原点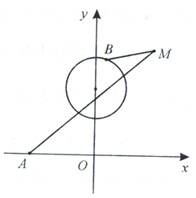 已知以原点
已知以原点