题目内容
（本题满分12分）已知函数f(x)=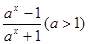
,
(1)判断函数的奇偶性；(2)证明f(x)是R上的增函数； (3)求该函数的值域；
【答案】
（1）是奇函数；（2）见解析；（3）（-1，1）；
【解析】(1)先确定定义域为R，关于原点对称，再判断f(-x)=-f(x)和f(-x)=f(x)那个成立，最终确定其是奇函数还是偶函数。
（2）利用单调性定义证明：第一步取值：设
，第二步：作差变形判断差值
符号,第三步得出结论。
（1）∵定义域为x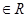
,且f(-x)=
是奇函数；
（2）设，
，
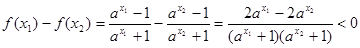
(∵分母大于零，且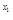a
<a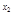
)
∴f(x)是R上的增函数。
（3）
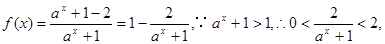即f(x)的值域为（-1，1）；
练习册系列答案
一本好题口算题卡系列答案
相关题目
的三个内角
、
、
所对的边分别为
、
、
.
，且
.（1）求
.求
.
，
的等比中项。
是等差数列；（2）若
的前n项和为Tn,求Tn。
：
的长轴长是短轴长的
倍，
，
是它的左，右焦点．
，且
，
，求
作以
（
是切点），且使
，求动点
的长轴，短轴端点分别是A,B，从椭圆上一点M向x轴作垂线，恰好通过椭圆的左焦点，向量
与
是共线向量
分别是左右焦点，求
的取值范围