题目内容
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为 .点P(1,
.点P(1, )、A、B在椭圆E上,且
)、A、B在椭圆E上,且 +
+ =m
=m (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)当m=-3时,证明原点O是△PAB的重心,并求直线AB的方程.
解:(1)设椭圆方程为 (a>b>0)
(a>b>0)
∵椭圆的离心率为 ,点P(1,
,点P(1, )在椭圆E上,
)在椭圆E上,
∴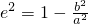 =
= 及
及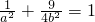
∴a2=4,b2=3,
∴椭圆方程为 ;
;
设A(x1,y1)、B(x2,y2),由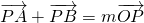 得(x1+x2-2,y1+y2-3)=m(1,
得(x1+x2-2,y1+y2-3)=m(1, ),即
),即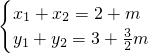
又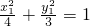 ,
, ,
,
两式相减得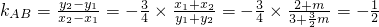 ;
;
(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足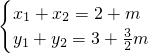 ,
,
点P的坐标为(1, ),m=-3,于是x1+x2+1=3+m=0,y1+y2+
),m=-3,于是x1+x2+1=3+m=0,y1+y2+ =3+
=3+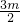 +
+ =0,
=0,
因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
∵x1+x2=-1,y1+y2=- ,∴AB中点坐标为(
,∴AB中点坐标为( ,
, ),
),
又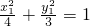 ,
, ,两式相减得
,两式相减得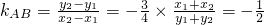 ;
;
∴直线AB的方程为y+ =
= (x+
(x+ ),即x+2y+2=0.
),即x+2y+2=0.
分析:(1)设椭圆方程为 (a>b>0),利用椭圆的离心率为
(a>b>0),利用椭圆的离心率为 ,点P(1,
,点P(1, )在椭圆E上,可求几何量,从而可得椭圆方程,设A(x1,y1)、B(x2,y2),由
)在椭圆E上,可求几何量,从而可得椭圆方程,设A(x1,y1)、B(x2,y2),由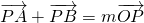 ,结合点差法,即可求得直线AB的斜率;
,结合点差法,即可求得直线AB的斜率;
(2)证明△PAB的重心坐标为(0,0)即可,确定AB中点坐标,点差法求直线AB的斜率,即可求得直线AB的方程.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查点差法求直线的斜率,正确运用椭圆方程是关键.
 (a>b>0)
(a>b>0)∵椭圆的离心率为
 ,点P(1,
,点P(1, )在椭圆E上,
)在椭圆E上,∴
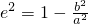 =
= 及
及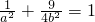
∴a2=4,b2=3,
∴椭圆方程为
 ;
;设A(x1,y1)、B(x2,y2),由
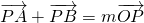 得(x1+x2-2,y1+y2-3)=m(1,
得(x1+x2-2,y1+y2-3)=m(1, ),即
),即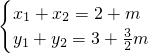
又
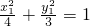 ,
, ,
,两式相减得
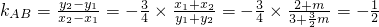 ;
;(2)由(1)知,点A(x1,y1)、B(x2,y2)的坐标满足
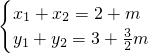 ,
,点P的坐标为(1,
 ),m=-3,于是x1+x2+1=3+m=0,y1+y2+
),m=-3,于是x1+x2+1=3+m=0,y1+y2+ =3+
=3+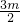 +
+ =0,
=0,因此△PAB的重心坐标为(0,0).即原点是△PAB的重心.
∵x1+x2=-1,y1+y2=-
 ,∴AB中点坐标为(
,∴AB中点坐标为( ,
, ),
),又
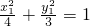 ,
, ,两式相减得
,两式相减得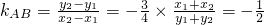 ;
;∴直线AB的方程为y+
 =
= (x+
(x+ ),即x+2y+2=0.
),即x+2y+2=0.分析:(1)设椭圆方程为
 (a>b>0),利用椭圆的离心率为
(a>b>0),利用椭圆的离心率为 ,点P(1,
,点P(1, )在椭圆E上,可求几何量,从而可得椭圆方程,设A(x1,y1)、B(x2,y2),由
)在椭圆E上,可求几何量,从而可得椭圆方程,设A(x1,y1)、B(x2,y2),由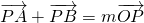 ,结合点差法,即可求得直线AB的斜率;
,结合点差法,即可求得直线AB的斜率;(2)证明△PAB的重心坐标为(0,0)即可,确定AB中点坐标,点差法求直线AB的斜率,即可求得直线AB的方程.
点评:本题考查椭圆的标准方程,考查向量知识的运用,考查点差法求直线的斜率,正确运用椭圆方程是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目