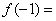题目内容
定义在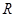 上的函数
上的函数
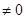 ,当
,当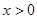 时,
时, ,且对任意的
,且对任意的 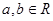 ,有
,有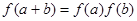 ,
,
(Ⅰ)求证: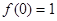 ;
;
(Ⅱ)求证:对任意的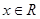 ,恒有
,恒有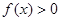 ;
;
(Ⅲ)证明: 是
是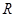 上的增函数.
上的增函数.
【答案】
(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)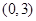 .
.
【解析】
试题分析:(Ⅰ)令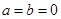 即可得证;(Ⅱ)令
即可得证;(Ⅱ)令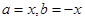 得,
得,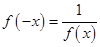 ,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明
,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明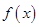 为增函数:任取x2>x1,则
为增函数:任取x2>x1,则 ,
,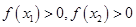 ,故
,故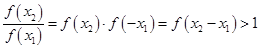 ,故其为增函数.
,故其为增函数.
试题解析:(Ⅰ)令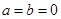 ,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
(Ⅱ)令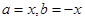 则
f(0)=f(x)f(-x) ∴
则
f(0)=f(x)f(-x) ∴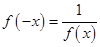 4分
4分
由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0
∴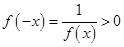 ,又x=0时,f(0)=1>0 6分
,又x=0时,f(0)=1>0 6分
∴ 对任意x∈R,f(x)>0 7分
(Ⅲ)任取x2>x1,则f(x2)>0,f(x1)>0,x2-x1>0 8分
∴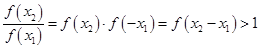
∴ f(x2)>f(x1) ∴ f(x)在R上是增函数 13分
考点:抽象函数、增函数的证明、一元二次不等式解法.

练习册系列答案
相关题目
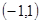 上的函数
上的函数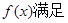
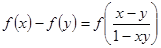 ;当
;当 时,
时,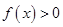 ,若
,若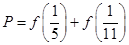 ,
,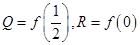 ,则P,Q,R的大小关系为( )
,则P,Q,R的大小关系为( )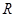 上的函数
上的函数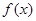 满足
满足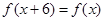 .当
.当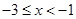 时,
时,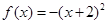 ,当
,当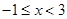 时,
时,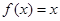 。则
。则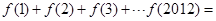 ( )
( )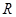 上的函数
上的函数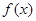 满足
满足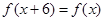 .当
.当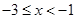 时,
时,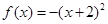 ,当
,当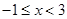 时,
时,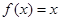 。则
。则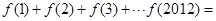
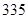 (B)
(B)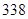 (C)
(C)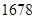 (D)
(D)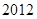
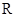 上的函数
上的函数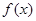 满足
满足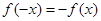 ,当
,当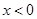 时,
时,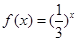 ,则
,则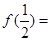
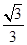 B.
B.
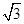 C.
C.
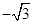 D.
D.
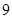
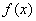 为定义在
为定义在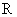 上的函数。当
上的函数。当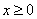 时,
时,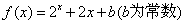 ,则
,则