题目内容
已知函数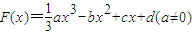 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.(Ⅰ)若y=F(x)在x=-1处取得极大值2,求函数y=F(x)的单调区间;
(Ⅱ)若使g(x)=0的x值满足
 ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.
【答案】分析:(Ⅰ)求F(x)的解析式,只需得到含两个a,b的等式,根据函数F(x)在x=-1处有极大值,可知,函数在x=-1处导数等于0,根据极大值为2,可知,x=-1时,函数值等于7,这样,就可求出a,b.对函数求导,再令导数大于0,解出x的范围,为函数的增区间,令导数小于0,解出x的范围,为函数的减区间.
(Ⅱ)由题意,f(x)=ax2-2bx+c=ax2-(a+c)x+c,,g(x)=2ax-2b=2ax-(a+c),联立可得ax2-(3a+c)x+a+2c=0,利用韦达定理,可求线段AB在x轴上的射影长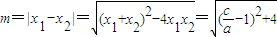 .从而可求线段AB在x轴上的射影长的取值范围.
.从而可求线段AB在x轴上的射影长的取值范围.
解答:解:∵F(x)的图象过原点,∴d=0.
又f(x)=F'(x)=ax2-2bx+c,f(1)=0,,∴a+c=2b.…①…(2分)
(Ⅰ)由y=F(x)在x=-1处取得极大值2知:f(-1)=a+2b+c=0,…②
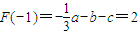 ,…③…(4分)
,…③…(4分)
由①②③得解:a=3,b=0,c=-3,
∴F(x)=x3-3x.…(5分)
由f(x)=3x2-3≥0,得x≥1或x≤-1;由f(x)=3x2-3≤0,得-1≤x≤1.
∴F(x)的单调递减区间为[-1,1],单调递增区间为(-∞,-1]和[1,+∞).…(7分)
(Ⅱ)f(x)=ax2-2bx+c=ax2-(a+c)x+c,,g(x)=2ax-2b=2ax-(a+c),
由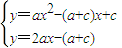 ,得ax2-(3a+c)x+a+2c=0.…(8分)
,得ax2-(3a+c)x+a+2c=0.…(8分)
设A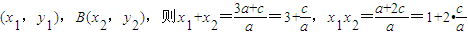 ,
,
∴线段AB在x轴上的射影长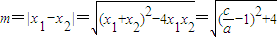 .…(9分)
.…(9分)
由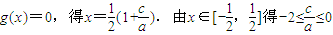 .…((10分)
.…((10分)
∴当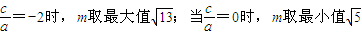 ,
,
∴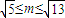 .…(12分)
.…(12分)
点评:本题以函数为载体,考查导数的运用,考查函数的极值,考查曲线相交,有一定的综合性.
(Ⅱ)由题意,f(x)=ax2-2bx+c=ax2-(a+c)x+c,,g(x)=2ax-2b=2ax-(a+c),联立可得ax2-(3a+c)x+a+2c=0,利用韦达定理,可求线段AB在x轴上的射影长
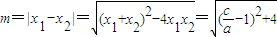 .从而可求线段AB在x轴上的射影长的取值范围.
.从而可求线段AB在x轴上的射影长的取值范围.解答:解:∵F(x)的图象过原点,∴d=0.
又f(x)=F'(x)=ax2-2bx+c,f(1)=0,,∴a+c=2b.…①…(2分)
(Ⅰ)由y=F(x)在x=-1处取得极大值2知:f(-1)=a+2b+c=0,…②
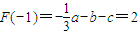 ,…③…(4分)
,…③…(4分)由①②③得解:a=3,b=0,c=-3,
∴F(x)=x3-3x.…(5分)
由f(x)=3x2-3≥0,得x≥1或x≤-1;由f(x)=3x2-3≤0,得-1≤x≤1.
∴F(x)的单调递减区间为[-1,1],单调递增区间为(-∞,-1]和[1,+∞).…(7分)
(Ⅱ)f(x)=ax2-2bx+c=ax2-(a+c)x+c,,g(x)=2ax-2b=2ax-(a+c),
由
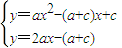 ,得ax2-(3a+c)x+a+2c=0.…(8分)
,得ax2-(3a+c)x+a+2c=0.…(8分)设A
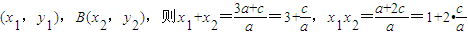 ,
,∴线段AB在x轴上的射影长
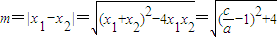 .…(9分)
.…(9分)由
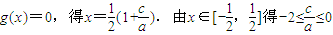 .…((10分)
.…((10分)∴当
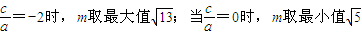 ,
,∴
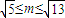 .…(12分)
.…(12分)点评:本题以函数为载体,考查导数的运用,考查函数的极值,考查曲线相交,有一定的综合性.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an. 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.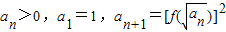 ,求数列an的通项公式an.
,求数列an的通项公式an.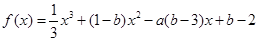 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组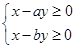 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .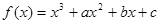 的图象过原点,且
的图象过原点,且 在
在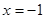 ,
, 处取得极值.
处取得极值.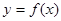 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.