题目内容
已知函数 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称.(1)求函数f(x)的解析式;
(2)若数列an(n∈N*)满足:
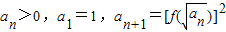 ,求数列an的通项公式an.
,求数列an的通项公式an.
【答案】分析:(1)因为函数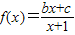 的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.
的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.
(2)由(1)的结论,可以得到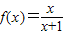 ,故可得
,故可得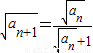 ,即
,即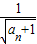 =
=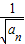 +1,所以
+1,所以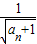 -
-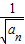 =1由此可以得到 数列{
=1由此可以得到 数列{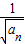 }的性质的,可求数列an的通项公式.
}的性质的,可求数列an的通项公式.
解答:解:(1)因为函数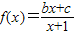 的图象过原点,即f(0)=0,所以c=0,即
的图象过原点,即f(0)=0,所以c=0,即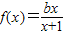 .
.
又函数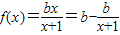 的图象关于点(-1,1)成中心对称,所以b=1,
的图象关于点(-1,1)成中心对称,所以b=1,
∴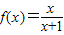 .
.
(2)∵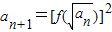 ,由(1)的结论开方得:
,由(1)的结论开方得: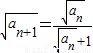 ,
,
变形得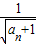 =
=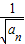 +1,所以
+1,所以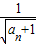 -
-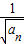 =1.
=1.
∴数列{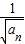 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.
∴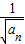 =1+(n-1)=n,即
=1+(n-1)=n,即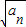 =
=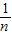 ,
,
∴an=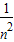 .
.
点评:本题考点是奇偶函数的图象的对称性,考查利用函数的对称性求求解析式,在第二问中用到了间接法求数列的通项公式,变形技巧值在学习中借鉴.
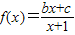 的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.
的图象过原点,即f(0)=0,可以解出c=0,再有对称性可以求出b值,即得函数的解析式.(2)由(1)的结论,可以得到
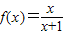 ,故可得
,故可得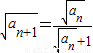 ,即
,即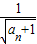 =
=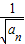 +1,所以
+1,所以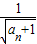 -
-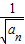 =1由此可以得到 数列{
=1由此可以得到 数列{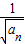 }的性质的,可求数列an的通项公式.
}的性质的,可求数列an的通项公式.解答:解:(1)因为函数
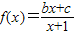 的图象过原点,即f(0)=0,所以c=0,即
的图象过原点,即f(0)=0,所以c=0,即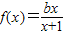 .
.又函数
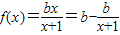 的图象关于点(-1,1)成中心对称,所以b=1,
的图象关于点(-1,1)成中心对称,所以b=1,∴
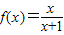 .
.(2)∵
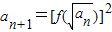 ,由(1)的结论开方得:
,由(1)的结论开方得: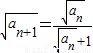 ,
,变形得
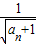 =
=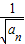 +1,所以
+1,所以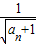 -
-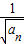 =1.
=1.∴数列{
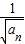 }是以1为首项,1为公差的等差数列.
}是以1为首项,1为公差的等差数列.∴
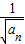 =1+(n-1)=n,即
=1+(n-1)=n,即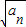 =
=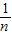 ,
,∴an=
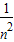 .
.点评:本题考点是奇偶函数的图象的对称性,考查利用函数的对称性求求解析式,在第二问中用到了间接法求数列的通项公式,变形技巧值在学习中借鉴.

练习册系列答案
相关题目
 的图象过原点,且关于点(-1,1)成中心对称.
的图象过原点,且关于点(-1,1)成中心对称. ,求数列an的通项公式an.
,求数列an的通项公式an.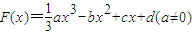 的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B.
的图象过原点,f(x)=F′(x),g(x)=f′(x),f(1)=0,函数y=f(x)与y=g(x)的图象交于不同的两点A、B. ,求线段AB在x轴上的射影长的取值范围.
,求线段AB在x轴上的射影长的取值范围.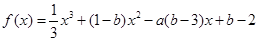 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是 ,则不等式组
,则不等式组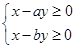 所确定的平面区域在
所确定的平面区域在 内的面积为 .
内的面积为 .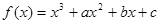 的图象过原点,且
的图象过原点,且 在
在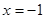 ,
, 处取得极值.
处取得极值.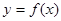 与
与 的图象有且仅有一个公共点,求实数
的图象有且仅有一个公共点,求实数 的取值范围.
的取值范围.