��Ŀ����
����Ŀ��������ʵ����k��b��ʹ�ú���F��x����G��x�����乫���������ϵ�����ʵ��x�����㣺F��x����kx+b��G��x����kx+b���������ƴ�ֱ��y=kx+bΪF��x����G��x���ġ�����ֱ�ߡ�����֪����f��x��=x2��x��R����g��x��= ![]() ��x��0����h��x��=2elnx�����������⣺
��x��0����h��x��=2elnx�����������⣺
��F��x��=f��x����g��x���� ![]() �ڵ���������
�ڵ���������
��f��x����g��x��֮����ڡ�����ֱ�ߡ�����b����СֵΪ��4��
��f��x����g��x��֮����ڡ�����ֱ�ߡ�����k��ȡֵ��Χ�ǣ���4��0]��
��f��x����h��x��֮�����Ψһ�ġ�����ֱ�ߡ�y=2 ![]() x��e��
x��e��
����������ĸ���Ϊ������������ȷ�������ţ�
���𰸡��٢ڢ�
���������⣺�١�F��x��=f��x����g��x��=x2�� ![]() ����x�ʣ���
����x�ʣ��� ![]() ��0����F�䣨x��=2x+
��0����F�䣨x��=2x+ ![]() ��0����F��x��=f��x����g��x����x�ʣ���
��0����F��x��=f��x����g��x����x�ʣ��� ![]() ��0���ڵ����������ʢٶԣ�
��0���ڵ����������ʢٶԣ�
�ڡ�����f��x����g��x���ĸ���ֱ��Ϊy=kx+b����x2��kx+b��һ��ʵ��x���������С�1��0��k2+4b��0��
�� ![]() ��kx+b��һ��x��0��������kx2+bx��1��0������2��0��b2+4k��0��k��0��b��0��
��kx+b��һ��x��0��������kx2+bx��1��0������2��0��b2+4k��0��k��0��b��0��
����k2�ܩ�4b��b2�ܩ�4k��k4��16b2�ܩ�64k��4��k��0��ͬ����4��b��0���ʢڶԣ��۴���
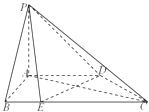
�ܺ���f��x����h��x����ͼ����x= ![]() ���й����㣬��˴���f��x����g��x���ĸ���ֱ�ߣ�
���й����㣬��˴���f��x����g��x���ĸ���ֱ�ߣ�
��ô��ֱ�߹���������㣬�����ֱ�ߵ�б��Ϊk�������ֱ�߷���Ϊy��e=k��x�� ![]() ������y=kx��k
������y=kx��k ![]() +e��
+e��
��f��x����kx��k ![]() +e��x��R�����ɵ�x2��kx+k
+e��x��R�����ɵ�x2��kx+k ![]() ��e��0��x��R�������
��e��0��x��R�������
�����0��ֻ��k=2 ![]() ����ʱֱ�߷���Ϊ��y=2
����ʱֱ�߷���Ϊ��y=2 ![]() x��e��
x��e��
����֤��h��x����2 ![]() x��e����G��x��=2
x��e����G��x��=2 ![]() x��e��h��x��=2
x��e��h��x��=2 ![]() x��e��2elnx��
x��e��2elnx��
G�䣨x��= 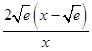 ��
��
��x= ![]() ʱ��G�䣨x��=0����0��x��
ʱ��G�䣨x��=0����0��x�� ![]() ʱ��G�䣨x����0����x��
ʱ��G�䣨x����0����x�� ![]() ʱ��G�䣨x����0��
ʱ��G�䣨x����0��
��x= ![]() ʱ��G��x��ȡ����Сֵ����Сֵ��0��Ҳ����Сֵ��
ʱ��G��x��ȡ����Сֵ����Сֵ��0��Ҳ����Сֵ��
����G��x��=2 ![]() x��e��g��x����0����g��x����2
x��e��g��x����0����g��x����2 ![]() x��e��x��0ʱ�������
x��e��x��0ʱ�������
�ຯ��f��x����g��x������Ψһ�ĸ���ֱ��y=2 ![]() x��e���ʢ���ȷ��
x��e���ʢ���ȷ��
���Դ��ǣ��٢ڢܣ�
�����㾫����������Ҫ�������������ٶ���Ӧ�õ����֪ʶ�㣬��Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ������ȷ�����⣮

 ѧ���쳵�����ּ��ں�����ҵϵ�д�
ѧ���쳵�����ּ��ں�����ҵϵ�д� ��˼ά������ҵϵ�д�
��˼ά������ҵϵ�д�