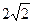题目内容
已知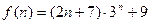 是否存在自然数
是否存在自然数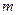 ,使对任意
,使对任意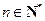 ,都有
,都有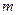 整除
整除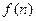 ?如果存在,求出
?如果存在,求出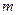 的最大值,并证明;若不存在,说明理由.
的最大值,并证明;若不存在,说明理由.
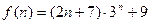 是否存在自然数
是否存在自然数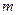 ,使对任意
,使对任意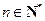 ,都有
,都有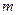 整除
整除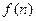 ?如果存在,求出
?如果存在,求出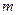 的最大值,并证明;若不存在,说明理由.
的最大值,并证明;若不存在,说明理由.36
解:由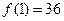 ,
, ,
, ,
,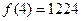 ,猜想
,猜想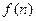 能被
能被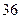 整除.
整除.
证明:(1)当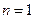 时,猜想显然成立.……………………………………………………2分
时,猜想显然成立.……………………………………………………2分
(2)假设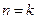 时,
时,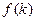 能被
能被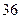 整除,即
整除,即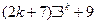 能被整除,…………………4分
能被整除,…………………4分
则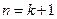 时,
时,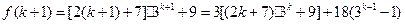 ,……6分
,……6分
根据假设可知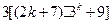 能被
能被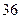 整除,而
整除,而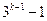 是偶数.
是偶数.
所以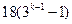 能被
能被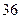 整除,从而
整除,从而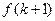 能被
能被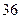 整除. …………………9分
整除. …………………9分
综上所述,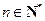 时,
时,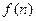 能被
能被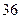 整除,由于
整除,由于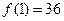
故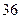 是整除
是整除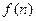 的自然数中的最大值
的自然数中的最大值
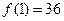 ,
, ,
, ,
,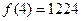 ,猜想
,猜想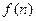 能被
能被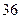 整除.
整除.证明:(1)当
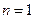 时,猜想显然成立.……………………………………………………2分
时,猜想显然成立.……………………………………………………2分(2)假设
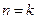 时,
时,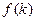 能被
能被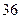 整除,即
整除,即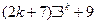 能被整除,…………………4分
能被整除,…………………4分则
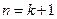 时,
时,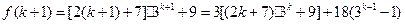 ,……6分
,……6分根据假设可知
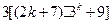 能被
能被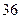 整除,而
整除,而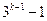 是偶数.
是偶数.所以
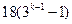 能被
能被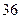 整除,从而
整除,从而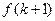 能被
能被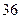 整除. …………………9分
整除. …………………9分综上所述,
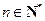 时,
时,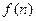 能被
能被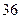 整除,由于
整除,由于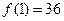
故
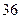 是整除
是整除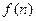 的自然数中的最大值
的自然数中的最大值
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
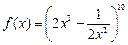
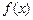 展开式中的常数项
展开式中的常数项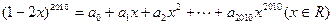 ,则
,则 __ _ ___.
__ _ ___.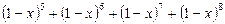 的展开式中,含
的展开式中,含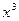 的项的系数是
的项的系数是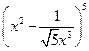 的展开式中的常数项为
的展开式中的常数项为 ,
,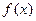 是以
是以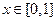 时,
时,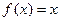 ,若在区间
,若在区间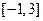 内,函数
内,函数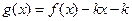 有4个零点,则
有4个零点,则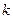 的取值范围是 .
的取值范围是 . 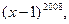 有下列命题:
有下列命题: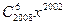 ;
;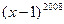 除以2008的余数是1.
除以2008的余数是1.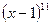 的展开式中含x偶数次幂的项的系数和是( )
的展开式中含x偶数次幂的项的系数和是( )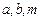 为正整数,若
为正整数,若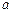 和
和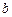 除以
除以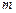 的余数相同,则称
的余数相同,则称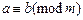 .已知
.已知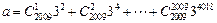 ,
,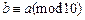 ,则
,则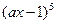 的展开式中
的展开式中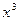 的系数是80,则实数
的系数是80,则实数 的值是
的值是