题目内容
对于函数y=f(x)(x∈D,D是此函数的定义域)若同时满足下列条件:
(Ⅰ)f(x)在D内单调递增或单调递减;
(Ⅱ)存在区间[a,b]![]() D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
D,使f(x)在[a,b]上的值域为[a,b];那么,把y=f(x)(x∈D)叫闭函数.
(1)求闭函数y=![]() 符合条件(Ⅱ)的区间[a,b];
符合条件(Ⅱ)的区间[a,b];
(2)判断函数f(x)=![]() (x∈
(x∈![]() )是否为闭函数?并说明理由;
)是否为闭函数?并说明理由;
(3)若y=![]() 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
答案:
解析:
解析:
解:(1)易知 注意到a<b,可得
(2)取 取 故f(x)不是(0,+∞)上的增函数 ∴ f(x)不是闭函数 (3)设函数 则 ∴ 命题等价于关于x的方程 当k≤-2时, ∴
当k>-2时 不合题意 ∴ k的取值范围为
|

练习册系列答案
相关题目
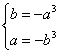
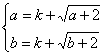 ∴ a,b为方程
∴ a,b为方程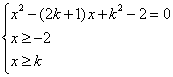 有两不等实根
有两不等实根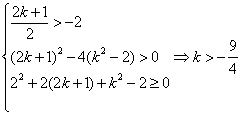 ∴
∴ 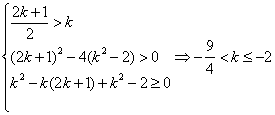
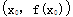 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: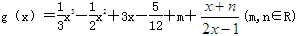 ,
,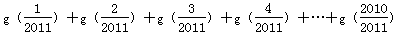 = .
= . 为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题:
为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心;且“拐点”就是对称中心.”请你根据这一发现,请回答问题: ,
, = .
= .