题目内容
若P:x≥2,Q:(x-2)
≥0,则P是Q的
| x+1 |
充分不必要
充分不必要
条件.分析:对充分性和必要性分别加以论证:当P成立时,根据x-2≥0且x+1≥3,可得Q成立,说明充分性成立;当Q成立时,解不等式得x=-1或x≥2,说明必要性不成立.由此可得正确选项.
解答:解:先看充分性
当P:x≥2成立时,
∵x-2≥0且x+1≥3
∴(x-2)
≥0,可得充分性成立;
再看必要性
当Q:(x-2)
≥0成立时,
可得x-2≥0或x+1=0,所以x=-1或x≥2,说明必要性不成立
综上所述,P是Q充分不必要条件
故答案为:充分不必要
当P:x≥2成立时,
∵x-2≥0且x+1≥3
∴(x-2)
| x+1 |
再看必要性
当Q:(x-2)
| x+1 |
可得x-2≥0或x+1=0,所以x=-1或x≥2,说明必要性不成立
综上所述,P是Q充分不必要条件
故答案为:充分不必要
点评:本题以含有根号的不等式的解法为载体,考查了充分条件、必要条件与充要条件的判断与应用,属于基础题.在解含有等号的不等式时,一定要看清等号成立的x的取值,否则会出现漏解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
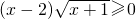 ,则P是Q的________条件.
,则P是Q的________条件.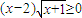 ,则P是Q的 条件.
,则P是Q的 条件.