题目内容
函数f(x)=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断其中正确的序号为
①若P∩M=∅,则f(P)∩f(M)=∅;
②若P∩M≠∅,则f(P)∩f(M)≠∅;
③若P∪M=R,则f(P)∪f(M)=R;
④若P∪M≠R,则f(P)∪f(M)≠R.
|
②④
②④
:①若P∩M=∅,则f(P)∩f(M)=∅;
②若P∩M≠∅,则f(P)∩f(M)≠∅;
③若P∪M=R,则f(P)∪f(M)=R;
④若P∪M≠R,则f(P)∪f(M)≠R.
分析:根据函数f(x)=
,可借助两个函数y=x与y=-x图象来研究,分析可得答案.
|
解答: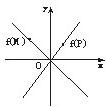 解:由题意知函数f(P)、f(M)的图象如图所示.
解:由题意知函数f(P)、f(M)的图象如图所示.
设P=[x2,+∞),M=(-∞,x1],
∵|x2|<|x1|,f(P)=[f(x2),+∞),f(M)=[f(x1),+∞),∴P∩M=∅.
而f(P)∩f(M)=[f(x1),+∞)≠∅,故①错误.
同理可知②正确.
设P=[x1,+∞),M=(-∞,x2],
∵|x2|<|x1|,则P∪M=R.
f(P)=[f(x1),+∞),f(M)=[f(x2),+∞),
f(P)∪f(M)=[f(x1),+∞)≠R,故③错误.
④若P∪M≠R,则f(P)∪f(M)≠R.这是不对的
∵f(x)是函数,对于定义域内的值x,都有唯一确定的值与之对应.
∴在x∈P∩M的时候,x=-x,即x只能为0,
也就是说,P和M若有交集,则只能为{0}
若要让f(x)取到R上每一个点,就要求定义域在R上不能有遗漏,
∴P∪M≠R时,必定f(P)∪f(M)≠R,故④正确
故答案为:②④
 解:由题意知函数f(P)、f(M)的图象如图所示.
解:由题意知函数f(P)、f(M)的图象如图所示.设P=[x2,+∞),M=(-∞,x1],
∵|x2|<|x1|,f(P)=[f(x2),+∞),f(M)=[f(x1),+∞),∴P∩M=∅.
而f(P)∩f(M)=[f(x1),+∞)≠∅,故①错误.

同理可知②正确.
设P=[x1,+∞),M=(-∞,x2],
∵|x2|<|x1|,则P∪M=R.
f(P)=[f(x1),+∞),f(M)=[f(x2),+∞),
f(P)∪f(M)=[f(x1),+∞)≠R,故③错误.
④若P∪M≠R,则f(P)∪f(M)≠R.这是不对的
∵f(x)是函数,对于定义域内的值x,都有唯一确定的值与之对应.
∴在x∈P∩M的时候,x=-x,即x只能为0,
也就是说,P和M若有交集,则只能为{0}
若要让f(x)取到R上每一个点,就要求定义域在R上不能有遗漏,
∴P∪M≠R时,必定f(P)∪f(M)≠R,故④正确
故答案为:②④
点评:本题考查对题设条件的理解与转化能力,借助图形的直观来来帮助判断命题的正误,以形助数,是解题的关键.

练习册系列答案
相关题目
探究函数f(x)=x+
x∈(0,+∞)的最小值,并确定相应的x的值,列表如下,请观察表中y值随x值变化的特点,完成下列问题:
(1)若当x>0时,函数f(x)=x+
时,在区间(0,2)上递减,则在 上递增;
(2)当x= 时,f(x)=x+
,x>0的最小值为 ;
(3)试用定义证明f(x)=x+
,x>0在区间上(0,2)递减;
(4)函数f(x)=x+
,x<0有最值吗?是最大值还是最小值?此时x为何值?
解题说明:(1)(2)两题的结果直接填写在答题卷中横线上;(4)题直接回答,不需证明.
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.102 | 4.24 | 4.3 | 5 | 5.8 | 7.57 | … |
| 4 |
| x |
(2)当x=
| 4 |
| x |
(3)试用定义证明f(x)=x+
| 4 |
| x |
(4)函数f(x)=x+
| 4 |
| x |
解题说明:(1)(2)两题的结果直接填写在答题卷中横线上;(4)题直接回答,不需证明.