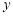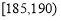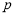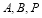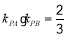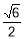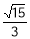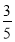题目内容
从某校高二年级 名男生中随机抽取
名男生中随机抽取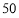 名学生测量其身高,据测量被测学生的身高全部在
名学生测量其身高,据测量被测学生的身高全部在 到
到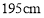 之间.将测量结果按如下方式分成
之间.将测量结果按如下方式分成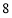 组:第一组
组:第一组 ,第二组
,第二组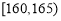 , ,第八组
, ,第八组 ,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
,如下右图是按上述分组得到的频率分布直方图的一部分.已知第一组与第八组的人数相同,第六组、第七组和第八组的人数依次成等差数列.
频率分布表如下:
分组 | 频数 | 频率 | 频率/组距 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
频率分布直方图如下:
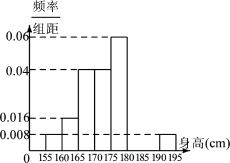
(1)求频率分布表中所标字母的值,并补充完成频率分布直方图;
(2)若从身高属于第六组和第八组的所有男生中随机抽取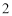 名男生,记他们的身高分别为
名男生,记他们的身高分别为 ,求满足:
,求满足: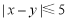 的事件的概率.
的事件的概率.
(1)详见解析;(2)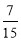 .
.
【解析】
试题分析:(1)由频率和为1,及题设条件得出样本中6、7组的人数为7人,由已知:x+m=7,x,m,2成等差数列,故可求得答案.
(2) 从身高属于第6组和第8组的所有男生中随机的抽取2名男生,记他们的身高分别为x、y,求满足:|x-y|≤5事件的概率,这是一个古典概率模型的问题.用列举法列出基本事件的个数与事件工包含的基本事件数,用古典概率模型的公式求概率..
试题解析:(1) 由频率分布直方图得前五组的频率是
 ,
,
第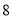 组的频率是
组的频率是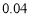 ,所以第
,所以第 组的频率是
组的频率是 ,所以样本中第
,所以样本中第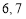 组的总人数为
组的总人数为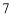 人.由已知得:
人.由已知得: 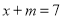 ①
①
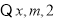 成等差数列,
成等差数列,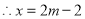 ②
②
由①②得: ,所以
,所以 4分
4分
频率分布直方图如下图所示:
 6分
6分
(2)由(1)知,身高在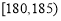 内的有
内的有 人,设为
人,设为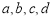 ,身高在
,身高在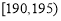 内的有
内的有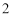 人,设为
人,设为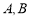
若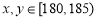 ,则有
,则有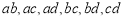 共
共 种情况;
种情况;
若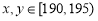 ,则有
,则有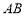 共
共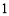 种情况;
种情况;
若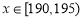 ,
,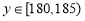 或
或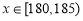 ,
,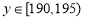 ,则有
,则有
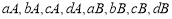 共
共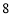 种情况
种情况
∴基本事件总数为 ,而事件 “
,而事件 “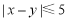 ”所包含的基本事件数为
”所包含的基本事件数为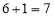 ,故
,故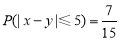 . 14分
. 14分
考点:1.频率分布直方图;2.等可能事件的概率..

练习册系列答案
相关题目