题目内容
求过点A（2，3）且被两直线3x+4y-7=0，3x+4y+8=0截得线段为3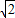
的直线方程．
【答案】分析：由条件求得∠MNB=45°，即2条直线的夹角为45°，故有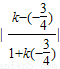 
=tan45°=1，解得k的值，用点斜式求得所求直线的方程．
解答：解：设所求直线l的斜率为k，∵|MN|=3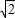
，又在Rt△MNB中，|MB|=3，∴∠MNB=45°，即2条直线的夹角为45°，
∴
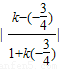=tan45°=1，解得 k=
，或k=-7，
所求直线的方程为y-3=
（x-2），或 y-3=-7（x-2），即 x-7y+19=0，或 7x+y-17=0．
点评：本题主要考查两条直线的夹角公式的应用，用点斜式求直线的方程，属于中档题．
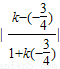=tan45°=1，解得k的值，用点斜式求得所求直线的方程．解答：解：设所求直线l的斜率为k，∵|MN|=3
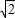，又在Rt△MNB中，|MB|=3，∴∠MNB=45°，即2条直线的夹角为45°，∴
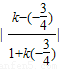=tan45°=1，解得 k=，或k=-7，所求直线的方程为y-3=
（x-2），或 y-3=-7（x-2），即 x-7y+19=0，或 7x+y-17=0．点评：本题主要考查两条直线的夹角公式的应用，用点斜式求直线的方程，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目