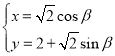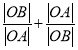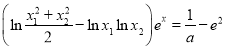题目内容
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,是否存在这样的点
,是否存在这样的点![]() 使得直线
使得直线![]() 与曲线
与曲线![]() 也相切,若存在,判断满足条件的点
也相切,若存在,判断满足条件的点![]() 的个数,若不存在,请说明理由.
的个数,若不存在,请说明理由.
【答案】(1)见解析;(2)存在,有且只有两个
【解析】
(1)利用导数的运算法则得出![]() ,分
,分![]() ,
,![]() ,
,![]() ,
,![]() 讨论单调性,分别解出
讨论单调性,分别解出![]() 与
与![]() 的区间即可得出单调区间.
的区间即可得出单调区间.
(2)先求直线![]() 为函数的图象上一点
为函数的图象上一点![]() 处的切线方程,再设直线
处的切线方程,再设直线![]() 与
与![]() 的图象也相切,切点为
的图象也相切,切点为![]() ,进而可得
,进而可得![]() ,再判断方程在区间
,再判断方程在区间![]() 上有且只有两个实数根.
上有且只有两个实数根.
(1)因为:![]() ,
,
所以:![]() .
.
所以:①当![]() 时:
时:![]() 在
在![]() 上为减函数,在
上为减函数,在![]() 为增函数;
为增函数;
②当![]() 时:
时:![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,在
上为减函数,在![]() 上为增函数;
上为增函数;
③当![]() 时:
时:![]() 在
在![]() 上为增函数;
上为增函数;
④当![]() 时:
时:![]() 在
在![]() 上为增函数,在
上为增函数,在![]() 上为减函数,在
上为减函数,在![]() 上为增函数.
上为增函数.
(2)设![]() .
.
因为:![]() ,所以:
,所以:![]() .
.
所以直线![]() 的方程为:
的方程为:![]() ,即:
,即:![]() ①.
①.
假设直线![]() 与
与![]() 的图象也相切,切点为:
的图象也相切,切点为:![]() .
.
因为![]() ,所以
,所以![]() .
.
所以直线![]() 的方程也可以写作为:
的方程也可以写作为:![]() .
.
又因为![]() ,即:
,即:![]() .
.
所以直线![]() 的方程为:
的方程为: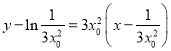 ,即:
,即:![]() ②.
②.
由①②有:![]() ,即:
,即:![]() .
.
令![]() ,
,
所以![]() .
.
令![]() ,得:
,得:![]() ,
,
所以![]() 在
在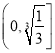 递减,在
递减,在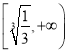 递增.
递增.
所以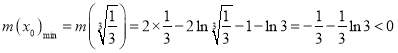 ,
,
又因为当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 有且只有两个实数根.
有且只有两个实数根.
所以,存在这样的点![]() 使得直线
使得直线![]() 与函数
与函数![]() 的图象也相切,这样的点
的图象也相切,这样的点![]() 有且只有两个.
有且只有两个.

【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: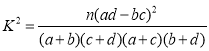 ,其中
,其中![]() .
.
【题目】自由购是通过自助结算方式购物的一种形式. 某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 |
|
|
|
|
| 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取 1 名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.