题目内容
已知点P是椭圆
上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2的角平分线上一点，且
，则|OM|的取值范围是（ ）A．（0，2
]B．
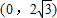
C．[2
）D．[0，4]
【答案】分析：结合椭圆的图象，当点P在椭圆与y轴交点处时，点M与原点O重合，此时|OM|取最小值0；当点P在椭圆与x轴交点处时，点M与焦点F1重合，此时|OM|取最大值2
，由此能够得到|OM|的取值范围．
解答：解：由题意得c=2
，当P在椭圆的短轴顶点处时，M与 O重合，|OM|取得最小值等于0．
当P在椭圆的长轴顶点处时，M与F1重合，|OM|取得最大值等于c=2
．
由于xy≠0，故|OM|的取值范围是
，
故选B．
点评：本题考查椭圆的定义、标准方程，以及简单性质的应用，结合图象解题，事半功倍．
，由此能够得到|OM|的取值范围．解答：解：由题意得c=2
，当P在椭圆的短轴顶点处时，M与 O重合，|OM|取得最小值等于0．当P在椭圆的长轴顶点处时，M与F1重合，|OM|取得最大值等于c=2
．由于xy≠0，故|OM|的取值范围是
，故选B．
点评：本题考查椭圆的定义、标准方程，以及简单性质的应用，结合图象解题，事半功倍．
练习册系列答案
相关题目
上的动点，F1，F2分别为其左、右焦点，O是坐标原点，则
的取值范围是
．
上的动点， F1，F2为椭圆的两个焦点，O是坐标原点，若M是
F1PF2平分线上的一点，且F1M
MP，则OM的取值范围是__________________。
上的动点，F1（-c，0）、F2（c，0）为椭圆的左、右焦点，O为坐标原点，若M是∠F1PF2的角平分线上的一点，且F1M⊥MP，则|OM|的取值范围是（ ）
上的动点，F1，F2为椭圆的两个焦点，O是坐标原点，若M是∠F1PF2平分线上的一点，且F1M⊥MP，则OM的取值范围是 ．