题目内容
已知球的表面积为 ,则该球的体积是 .
,则该球的体积是 .
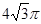
解析试题分析:球的表面积为 ,即4π
,即4π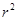 =12π,所以r=
=12π,所以r= 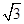 ,
,
故球的体积为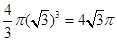 。
。
考点:本题主要考查球的几何特征,球的表面积及体积计算公式。
点评:简单题,从已知出发,先求球的半径,再计算体积。

练习册系列答案
相关题目
题目内容
已知球的表面积为 ,则该球的体积是 .
,则该球的体积是 .
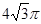
解析试题分析:球的表面积为 ,即4π
,即4π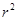 =12π,所以r=
=12π,所以r= 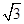 ,
,
故球的体积为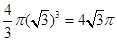 。
。
考点:本题主要考查球的几何特征,球的表面积及体积计算公式。
点评:简单题,从已知出发,先求球的半径,再计算体积。
