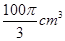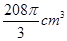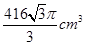题目内容
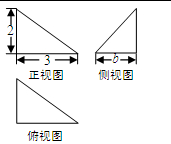
一简单组合体的三视图如图所示,则该组合体的体积为( )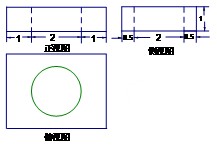
A.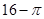 | B.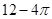 | C.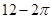 | D.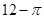 |
D
解析试题分析:由三视图可知,该几何体是在一个长方体中挖去一个圆柱而形成的,长方体的底面积为 ,高为
,高为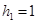 ,因此长方体的体积为
,因此长方体的体积为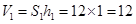 ,圆柱的底面是一个直径为
,圆柱的底面是一个直径为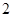 的圆,其半径长为
的圆,其半径长为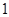 ,故其底面积为
,故其底面积为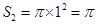 ,高为
,高为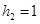 ,故圆柱的体积为
,故圆柱的体积为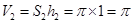 ,综上所述,该几何体的体积为
,综上所述,该几何体的体积为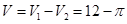 ,故选D.
,故选D.
考点:1.三视图;2.空间几何体的体积

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
个棱锥的三视图如上图,则该棱锥的全面积(单位:cm2)为( )
A.48+12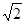 | B.48+24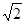 | C.36+12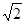 | D.36+24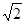 |
某几何体三视图如下图所示,则该几何体的体积是( )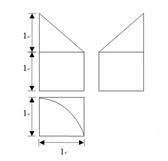
A.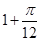 | B. | C.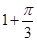 | D.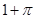 |
右图中的三个直角三角形是一个体积为 的几何体的三视图,则
的几何体的三视图,则 ( )
( )
A. | B. | C. | D. |
如图,在棱长为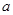 的正方体
的正方体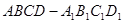 中,
中,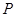 为
为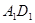 的中点,
的中点, 为
为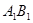 上任意一点,
上任意一点,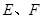 为
为 上任意两点,且
上任意两点,且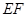 的长为定值,则下面四个值中不为定值的是
的长为定值,则下面四个值中不为定值的是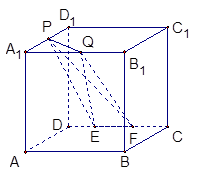
A.点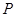 到平面 到平面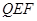 的距离 的距离 |
B.直线 与平面 与平面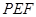 所成的角 所成的角 |
C.三棱锥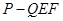 的体积 的体积 |
D.二面角 的大小 的大小 |
某三棱锥的主视图与俯视图如图所示,则其左视图的面积为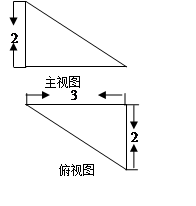
A. | B.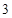 | C. | D.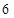 |
如图,正方体的底面与正四面体的底面在同一平面 上,且
上,且 ,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为
,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为 ,那么
,那么 ( )
( )
| A.8 |
| B.9 |
| C.10 |
| D.11 |
某空间几何体的三视图如图所示,则该几何体的表面积为( )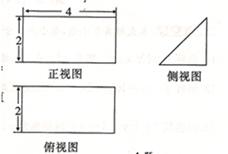
A.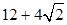 | B. | C. | D.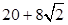 |