题目内容
本题满分12分）已知直线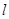
的参数方程为：
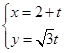（t为参数），曲线C的极坐标方程为：
．
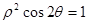（1）求直线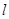被曲线C截得的弦长，
（2）若直线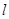与曲线C交于A、B两点，求线段AB的中点坐标.
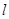的参数方程为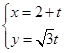：（t为参数），曲线C的极坐标方程为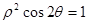：．（1）求直线
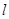被曲线C截得的弦长，（2）若直线
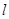与曲线C交于A、B两点，求线段AB的中点坐标.（1）
（2）
（2）
（1）由曲线
得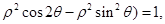
化成普通方程
① 5分
（2）方法一：把直线参数方程化为标准参数方程
（
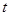为参数） ②把②代入①
整理，得
设其两根为
，则
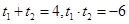8分
从而弦长为
10分
（2）由（1）当（*）中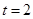
时为中点，中点为
思路分析：（1）把参数方程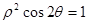，化为普通方程，直线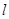的参数方程为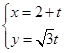：（t为参数），化为普通方程
，直线方程与双曲线方程联立消去得
，利用弦长公式解得弦长为
由韦达定理和（1）得线段AB的中点。
得
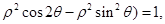化成普通方程 ① 5分（2）方法一：把直线参数方程化为标准参数方程
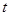（为参数） ②把②代入①整理，得
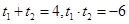设其两根为，则 8分从而弦长为
10分（2）由（1）当（*）中
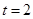时为中点，中点为思路分析：（1）把参数方程
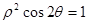，化为普通方程，直线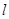的参数方程为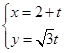：（t为参数），化为普通方程，直线方程与双曲线方程联立消去得，利用弦长公式解得弦长为由韦达定理和（1）得线段AB的中点。 
练习册系列答案
阅读快车系列答案
相关题目
为参数）与曲线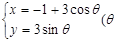
为参数）相交于A，B两点，则|AB|= 。
（
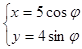为参数）； ⑵、
（
为参数）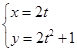
(
为参数)，则过曲线C上横坐标为1的点的切线方程为 .
(t为参数)上对应t="0," t=1两点间的距离是___________.
：
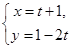(t为参数)与曲线
：
(
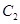为参数，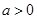
) 有一个公共点在X轴上，则
.
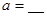为参数
化为普通方程．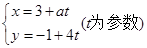
过定点_____________。