题目内容
已知正项等比数列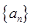 满足:
满足: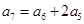 ,若存在两项
,若存在两项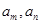 使得
使得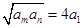 ,则
,则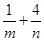 的最小值为 ;
的最小值为 ;
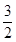
解析试题分析:因为数列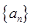 为正项等比数列,设公比为
为正项等比数列,设公比为 , 则
, 则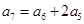
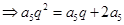
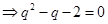 解得:
解得: 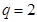 ,
,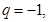 (舍)
(舍)
又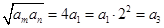 所以
所以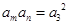 即
即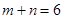
又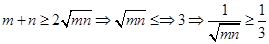
又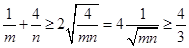
考点:等比数列的性质应用,基本不等式.

练习册系列答案
相关题目
题目内容
已知正项等比数列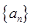 满足:
满足: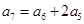 ,若存在两项
,若存在两项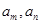 使得
使得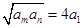 ,则
,则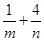 的最小值为 ;
的最小值为 ;
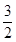
解析试题分析:因为数列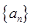 为正项等比数列,设公比为
为正项等比数列,设公比为 , 则
, 则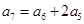
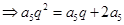
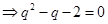 解得:
解得: 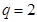 ,
,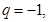 (舍)
(舍)
又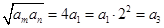 所以
所以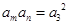 即
即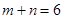
又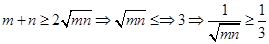
又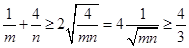
考点:等比数列的性质应用,基本不等式.
