题目内容
已知 ,M、N是双曲线上关于原点对称的两点,P是双曲线上任意一点,且直线PM,PN的斜率分别为k1、k2(k1k2≠0),若|k1|+|k2|的最小值为1,则双曲线的离心率为________.
,M、N是双曲线上关于原点对称的两点,P是双曲线上任意一点,且直线PM,PN的斜率分别为k1、k2(k1k2≠0),若|k1|+|k2|的最小值为1,则双曲线的离心率为________.

分析:先求出KPM•KPN =
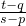 •
•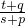 =
=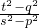 =
= ,再由|k1|+|k2|≥2
,再由|k1|+|k2|≥2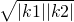 =2
=2  =1,即b=
=1,即b= ,
,由此求出e=
 的值.
的值.解答:设M(p,q),N(-p,-q),P(s,t),则有
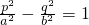 ,
,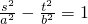 ,
,∴k1•k2=KPM•KPN=
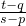 •
•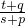 =
=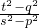 =
= .
.又|k1|+|k2|≥2
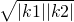 =2
=2  ,由题意可得 2•
,由题意可得 2• =1,∴b=
=1,∴b= ,
,∴e=
 =
=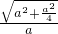 =
= ,
,故答案为
 .
.点评:本题考查双曲线的标准方程,以及双曲线的简单性质,基本不等式的应用,得到 KPM•KPN=
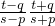
=
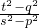 =
= ,是解题的关键.
,是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
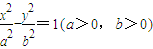 ,M、N是双曲线上关于原点对称的两点,P是双曲线上任意一点,且直线PM,PN的斜率分别为k1、k2(k1k2≠0),若|k1|+|k2|的最小值为1,则双曲线的离心率为 .
,M、N是双曲线上关于原点对称的两点,P是双曲线上任意一点,且直线PM,PN的斜率分别为k1、k2(k1k2≠0),若|k1|+|k2|的最小值为1,则双曲线的离心率为 .