题目内容
已知直线l1:y=x,l2:y=2x,l3:y=-x+6和l4:y=0,由l1,l2,l3围成的三角形区域记为D,一质点随机地落入由直线l2,l3,l4围成的三角形区域内,求质点落入区域D内的概率.
分析:本题考查的知识点是几何根据,根据l2,l3,l4围成的三角形区域,我们计算出满足条件的平面图形的面积,再由计算l1,l2,l3围成的三角形区域的面积,代入几何概型计算公式,即可得到答案.
解答: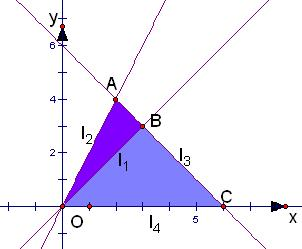 解:满足由直线l2,l3,l4围成的三角形区域的三角形,如图示的阴影部分(大三角形OAC),其中满足l1,l2,l3围成的三角形区域的三角形,如图示深色的阴影部分(小三角形OAB),A(2,4),B(3,3).
解:满足由直线l2,l3,l4围成的三角形区域的三角形,如图示的阴影部分(大三角形OAC),其中满足l1,l2,l3围成的三角形区域的三角形,如图示深色的阴影部分(小三角形OAB),A(2,4),B(3,3).
这两个三角形可看成是同底OC,故它们的面积之比等于对应的高的比.
故质点落入D中的概率P=
=
=1-
=1-
=1-
=
.
 解:满足由直线l2,l3,l4围成的三角形区域的三角形,如图示的阴影部分(大三角形OAC),其中满足l1,l2,l3围成的三角形区域的三角形,如图示深色的阴影部分(小三角形OAB),A(2,4),B(3,3).
解:满足由直线l2,l3,l4围成的三角形区域的三角形,如图示的阴影部分(大三角形OAC),其中满足l1,l2,l3围成的三角形区域的三角形,如图示深色的阴影部分(小三角形OAB),A(2,4),B(3,3).这两个三角形可看成是同底OC,故它们的面积之比等于对应的高的比.
故质点落入D中的概率P=
| S△OAB |
| S△OAC |
| S△OAC-S△OBC |
| S△OAC |
| S△OBC |
| S△OAC |
| xB |
| xA |
| 3 |
| 4 |
| 1 |
| 4 |
点评:几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据P=N(A)/N求解.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知直线l1:y=x,若直线l2⊥l1,则直线l2的倾斜角为( )
A、
| ||
B、kπ+
| ||
C、
| ||
D、kπ+
|
 平行,则a的值为( )
平行,则a的值为( )