题目内容
类比平面几何中的定理“设a,b,c是三条直线,若a⊥c,b⊥c,则a∥b”,得出如下结论:
①设a,b,c是空间的三条直线,若a⊥c,b⊥c,则a∥b;
②设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b;
③设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β;
④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β;
其中正确命题的个数是
- A.1
- B.2
- C.3
- D.4
B
分析:利用异面直线的概念与线面垂直的性质及面面垂直的性质对①②③④四个选项逐一判断即可.
解答:对于①,a,b,c是空间的三条直线,若a⊥c,b⊥c,则a与b可能平行,也可能相交,也可能异面,故①错误;
对于②,设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b,正确;
对于③,设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β,正确;
对于④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β,错误,如墙角的三个互相垂直的平面.
故正确答案为:②③.
故选B.
点评:本题考查命题的真假判断与应用,着重考查空间中直线与直线之间的位置关系,考查平面与平面之间的位置关系,属于中档题.
分析:利用异面直线的概念与线面垂直的性质及面面垂直的性质对①②③④四个选项逐一判断即可.
解答:对于①,a,b,c是空间的三条直线,若a⊥c,b⊥c,则a与b可能平行,也可能相交,也可能异面,故①错误;
对于②,设a,b是两条直线,α是平面,若a⊥α,b⊥α,则a∥b,正确;
对于③,设α,β是两个平面,m是直线,若m⊥α,m⊥β,则α∥β,正确;
对于④设α,β,γ是三个平面,若α⊥γ,β⊥γ,则α∥β,错误,如墙角的三个互相垂直的平面.
故正确答案为:②③.
故选B.
点评:本题考查命题的真假判断与应用,着重考查空间中直线与直线之间的位置关系,考查平面与平面之间的位置关系,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 是三条直线,若
是三条直线,若 ,则
,则 ∥
∥ ”,得出如下结论:
”,得出如下结论: 是两条直线,
是两条直线,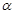 是平面,若
是平面,若 ,则
,则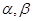 是两个平面,
是两个平面,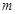 是直线,若
是直线,若 则
则 ;
;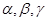 是三个平面,若
是三个平面,若 ,则
,则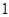 B.
B.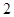 C.
C.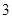 D.
D.